In music, 22 equal temperament, called 22-TET, 22-EDO, or 22-ET, is the tempered scale derived by dividing the octave into 22 equal steps (equal frequency ratios). ⓘ Each step represents a frequency ratio of 22√2, or 54.55 cents (ⓘ).
When composing with 22-ET, one needs to take into account a variety of considerations. Considering the 5-limit, there is a difference between 3 fifths and the sum of 1 fourth + 1 major third. It means that, starting from C, there are two A's - one 16 steps and one 17 steps away. There is also a difference between a major tone and a minor tone. In C major, the second note (D) will be 4 steps away. However, in A minor, where A is 6 steps below C, the fourth note (D) will be 9 steps above A, so 3 steps above C. So when switching from C major to A minor, one needs to slightly change the D note. These discrepancies arise because, unlike 12-ET, 22-ET does not temper out the syntonic comma of 81/80, but instead exaggerates its size by mapping it to one step.
Extending 22-ET to the 7-limit, we find the septimal minor seventh (7/4) can be distinguished from the sum of a fifth (3/2) and a minor third (6/5). Also the septimal subminor third (7/6) is different from the minor third (6/5). This mapping tempers out the septimal comma of 64/63, which allows 22-ET to function as a "Superpythagorean" system where four stacked fifths are equated with the septimal major third (9/7) rather than the usual pental third of 5/4. This system is a "mirror image" of septimal meantone in many ways: while meantone systems temper the fifth narrow so that intervals of 5 are simple while intervals of 7 are complex, Superpythagorean systems temper the fifth wide so that intervals of 7 are simple while intervals of 5 are complex. The enharmonic structure is also reversed: sharps are sharper than flats, similar to Pythagorean tuning, but to a greater degree.
Finally, 22-ET has a good approximation of the 11th harmonic, and is in fact the smallest equal temperament to be consistent in the 11-limit.
The net effect is that 22-ET allows (and to some extent even forces) the exploration of new musical territory, while still having excellent approximations of common practice consonances.
History and use
The idea of dividing the octave into 22 steps of equal size seems to have originated with nineteenth-century music theorist RHM Bosanquet. Inspired by the division of the octave into 22 unequal parts in the music theory of India, Bosanquet noted that an equal division was capable of representing 5-limit music with tolerable accuracy.[1] In this he was followed in the twentieth century by theorist José Würschmidt, who noted it as a possible next step after 19 equal temperament, and J. Murray Barbour in his survey of tuning history, Tuning and Temperament.[2] Contemporary advocates of 22 equal temperament include music theorist Paul Erlich.
Notation
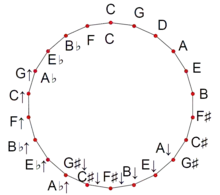
22-EDO can be notated several ways. The first, Ups And Downs Notation,[3] uses up and down arrows, written as a caret and a lower-case "v", usually in a sans-serif font. One arrow equals one edostep. In note names, the arrows come first, to facilitate chord naming. This yields the following chromatic scale:
C, ^C/D♭, vC♯/^D♭, C♯/vD,
D, ^D/E♭, vD♯/^E♭, D♯/vE, E,
F, ^F/G♭, vF♯/^G♭, F♯/vG,
G, ^G/A♭, vG♯/^A♭, G♯/vA,
A, ^A/B♭, vA♯/^B♭, A♯/vB, B, C
The pythagorean minor chord with 32/27 on C is still named Cm and still spelled C–E♭–G. But the 5-limit upminor chord uses the upminor 3rd 6/5 and is spelled C–^E♭–G. This chord is named C^m. Compare with ^Cm (^C–^E♭–^G).
The second, Quarter Tone Notation, uses half-sharps and half-flats instead of up and down arrows:
C, C![]() , C♯/D♭, D
, C♯/D♭, D![]() ,
,
D, D![]() , D♯/E♭, E
, D♯/E♭, E![]() , E,
, E,
F, F![]() , F♯/G♭, G
, F♯/G♭, G![]() ,
,
G, G![]() , G♯/A♭, A
, G♯/A♭, A![]() ,
,
A, A![]() , A♯/B♭, B
, A♯/B♭, B![]() , B, C
, B, C
However, chords and some enharmonic equivalences are much different than they are in 12-EDO. For example, even though a 5-limit C minor triad is notated as C–E♭–G, C major triads are now C–E![]() –G instead of C–E–G, and an A minor triad is now A–C
–G instead of C–E–G, and an A minor triad is now A–C![]() –E even though an A major triad is still A–C♯–E. Additionally, while major seconds such as C–D are divided as expected into 4 quarter tones, minor seconds such as E–F and B–C are 1 quarter tone, not 2. Thus E♯ is now equivalent to F
–E even though an A major triad is still A–C♯–E. Additionally, while major seconds such as C–D are divided as expected into 4 quarter tones, minor seconds such as E–F and B–C are 1 quarter tone, not 2. Thus E♯ is now equivalent to F![]() instead of F, F♭ is equivalent to E
instead of F, F♭ is equivalent to E![]() instead of E, F is equivalent to E
instead of E, F is equivalent to E![]() , and E is equivalent to F
, and E is equivalent to F![]() . Furthermore, the note a fifth above B is not the expected F♯ but rather F
. Furthermore, the note a fifth above B is not the expected F♯ but rather F![]() or G
or G![]() , and the note that is a fifth below F is now B
, and the note that is a fifth below F is now B![]() instead of B♭.
instead of B♭.
The third, Porcupine Notation, introduces no new accidentals, but significantly changes chord spellings (e.g. the 5-limit major triad is now C–E♯–G♯). In addition, enharmonic equivalences from 12-EDO are no longer valid. This yields the following chromatic scale:
C, C♯, D♭,
D, D♯, E♭,
E, E♯, F♭,
F, F♯, G♭,
G, G♯, G![]() /A
/A![]() , A♭,
A, A♯, B♭,
B, B♯, C♭, C
, A♭,
A, A♯, B♭,
B, B♯, C♭, C
Interval size
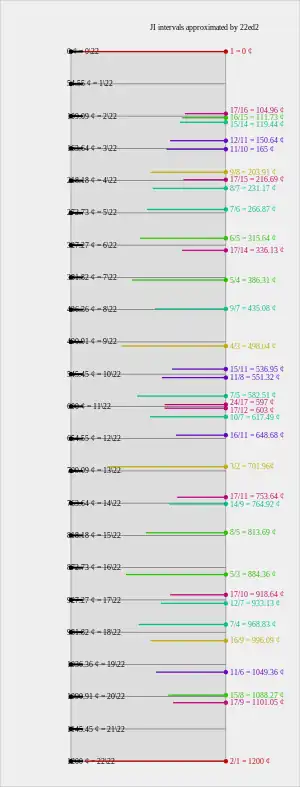
The table below gives the sizes of some common intervals in 22 equal temperament. An interval shown with a shaded background — such as the septimal tritone — is one that is more than 1/4 of a step (approximately 13.6 cents) out of tune, when compared to the just ratio it approximates.
| interval name | size (steps) | size (cents) | midi | just ratio | just (cents) | midi | error (cents) |
|---|---|---|---|---|---|---|---|
| octave | 22 | 1200 | 2:1 | 1200 | 0 | ||
| major seventh | 20 | 1090.91 | ⓘ | 15:8 | 1088.27 | ⓘ | +2.64 |
| septimal minor seventh | 18 | 981.818 | 7:4 | 968.82591 | +12.99 | ||
| 17:10 wide major sixth | 17 | 927.27 | ⓘ | 17:10 | 918.64 | +8.63 | |
| major sixth | 16 | 872.73 | ⓘ | 5:3 | 884.36 | ⓘ | −11.63 |
| perfect fifth | 13 | 709.09 | ⓘ | 3:2 | 701.95 | ⓘ | +7.14 |
| septendecimal tritone | 11 | 600.00 | ⓘ | 17:12 | 603.00 | −3.00 | |
| tritone | 11 | 600.00 | 45:32 | 590.22 | ⓘ | +9.78 | |
| septimal tritone | 11 | 600.00 | 7:5 | 582.51 | ⓘ | +17.49 | |
| 11:8 wide fourth | 10 | 545.45 | ⓘ | 11:8 | 551.32 | ⓘ | −5.87 |
| 375th subharmonic | 10 | 545.45 | 512:375 | 539.10 | +6.35 | ||
| 15:11 wide fourth | 10 | 545.45 | 15:11 | 536.95 | ⓘ | +8.50 | |
| perfect fourth | 9 | 490.91 | ⓘ | 4:3 | 498.05 | ⓘ | −7.14 |
| septendecimal supermajor third | 8 | 436.36 | ⓘ | 22:17 | 446.36 | −10.00 | |
| septimal major third | 8 | 436.36 | 9:7 | 435.08 | ⓘ | +1.28 | |
| diminished fourth | 8 | 436.36 | 32:25 | 427.37 | ⓘ | +8.99 | |
| undecimal major third | 8 | 436.36 | 14:11 | 417.51 | ⓘ | +18.86 | |
| major third | 7 | 381.82 | ⓘ | 5:4 | 386.31 | ⓘ | −4.49 |
| undecimal neutral third | 6 | 327.27 | ⓘ | 11:9 | 347.41 | ⓘ | −20.14 |
| septendecimal supraminor third | 6 | 327.27 | 17:14 | 336.13 | ⓘ | −8.86 | |
| minor third | 6 | 327.27 | 6:5 | 315.64 | ⓘ | +11.63 | |
| septendecimal augmented second | 5 | 272.73 | ⓘ | 20:17 | 281.36 | −8.63 | |
| augmented second | 5 | 272.73 | 75:64 | 274.58 | ⓘ | −1.86 | |
| septimal minor third | 5 | 272.73 | 7:6 | 266.88 | ⓘ | +5.85 | |
| septimal whole tone | 4 | 218.18 | ⓘ | 8:7 | 231.17 | ⓘ | −12.99 |
| diminished third | 4 | 218.18 | 256:225 | 223.46 | ⓘ | −5.28 | |
| septendecimal major second | 4 | 218.18 | 17:15 | 216.69 | +1.50 | ||
| whole tone, major tone | 4 | 218.18 | 9:8 | 203.91 | ⓘ | +14.27 | |
| whole tone, minor tone | 3 | 163.64 | ⓘ | 10:9 | 182.40 | ⓘ | −18.77 |
| neutral second, greater undecimal | 3 | 163.64 | 11:10 | 165.00 | ⓘ | −1.37 | |
| 1125th harmonic | 3 | 163.64 | 1125:1024 | 162.85 | +0.79 | ||
| neutral second, lesser undecimal | 3 | 163.64 | 12:11 | 150.64 | ⓘ | +13.00 | |
| septimal diatonic semitone | 2 | 109.09 | ⓘ | 15:14 | 119.44 | ⓘ | −10.35 |
| diatonic semitone, just | 2 | 109.09 | 16:15 | 111.73 | ⓘ | −2.64 | |
| 17th harmonic | 2 | 109.09 | 17:16 | 104.95 | ⓘ | +4.13 | |
| Arabic lute index finger | 2 | 109.09 | 18:17 | 98.95 | ⓘ | +10.14 | |
| septimal chromatic semitone | 2 | 109.09 | 21:20 | 84.47 | ⓘ | +24.62 | |
| chromatic semitone, just | 1 | 54.55 | ⓘ | 25:24 | 70.67 | ⓘ | −16.13 |
| septimal third-tone | 1 | 54.55 | 28:27 | 62.96 | ⓘ | −8.42 | |
| undecimal quarter tone | 1 | 54.55 | 33:32 | 53.27 | ⓘ | +1.27 | |
| septimal quarter tone | 1 | 54.55 | 36:35 | 48.77 | ⓘ | +5.78 | |
| diminished second | 1 | 54.55 | 128:125 | 41.06 | ⓘ | +13.49 |
See also
References
- ↑ Bosanquet, R.H.M. "On the Hindoo division of the octave, with additions to the theory of higher orders" (Archived 2009-10-22), Proceedings of the Royal Society of London vol. 26 (March 1, 1877, to December 20, 1877) Taylor & Francis, London 1878, pp. 372–384. (Reproduced in Tagore, Sourindro Mohun, Hindu Music from Various Authors, Chowkhamba Sanskrit Series, Varanasi, India, 1965).
- ↑ Barbour, James Murray, Tuning and temperament, a historical survey, East Lansing, Michigan State College Press, 1953 [c1951].
- ↑ "Ups_and_downs_notation", on Xenharmonic Wiki. Accessed 2023-8-12.
External links
- Erlich, Paul, "Tuning, Tonality, and Twenty-Two Tone Temperament", William A. Sethares.
- Pachelbel's Canon in 22edo (MIDI), Herman Miller
