Rhombitetraoctagonal tiling
Rhombitetraoctagonal tiling
Poincaré disk model of the hyperbolic plane
TypeHyperbolic uniform tiling
Vertex configuration4.4.8.4
Schläfli symbolrr{8,4} or
Wythoff symbol4 | 8 2
Coxeter diagram or
Symmetry group[8,4], (*842)
DualDeltoidal tetraoctagonal tiling
PropertiesVertex-transitive

In geometry, the rhombitetraoctagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of rr{8,4}. It can be seen as constructed as a rectified tetraoctagonal tiling, r{8,4}, as well as an expanded order-4 octagonal tiling or expanded order-8 square tiling.

Constructions

There are two uniform constructions of this tiling, one from [8,4] or (*842) symmetry, and secondly removing the mirror middle, [8,1+,4], gives a rectangular fundamental domain [∞,4,∞], (*4222).

Two uniform constructions of 4.4.4.8
Name Rhombitetraoctagonal tiling
Image
Symmetry [8,4]
(*842)
 [8,1+,4] = [∞,4,∞]
(*4222)
=
Schläfli symbol rr{8,4} t0,1,2,3{∞,4,∞}
Coxeter diagram =

Symmetry

A lower symmetry construction exists, with (*4222) orbifold symmetry. This symmetry can be seen in the dual tiling, called a deltoidal tetraoctagonal tiling, alternately colored here. Its fundamental domain is a Lambert quadrilateral, with 3 right angles.

The dual tiling, called a deltoidal tetraoctagonal tiling, represents the fundamental domains of the *4222 orbifold.

With edge-colorings there is a half symmetry form (4*4) orbifold notation. The octagons can be considered as truncated squares, t{4} with two types of edges. It has Coxeter diagram , Schläfli symbol s2{4,8}. The squares can be distorted into isosceles trapezoids. In the limit, where the rectangles degenerate into edges, an order-8 square tiling results, constructed as a snub tetraoctagonal tiling, .

*n42 symmetry mutation of expanded tilings: n.4.4.4
Symmetry
[n,4], (*n42)		 Spherical Euclidean Compact hyperbolic Paracomp.
*342
[3,4]		 *442
[4,4]		 *542
[5,4]		 *642
[6,4]		 *742
[7,4]		 *842
[8,4]		 *∞42
[∞,4]
Expanded
figures
Config. 3.4.4.4 4.4.4.4 5.4.4.4 6.4.4.4 7.4.4.4 8.4.4.4 ∞.4.4.4
Rhombic
figures
config.
V3.4.4.4
V4.4.4.4
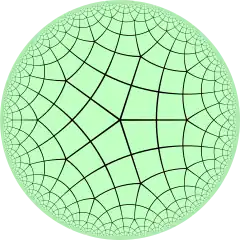V5.4.4.4
V6.4.4.4
V7.4.4.4
V8.4.4.4
V∞.4.4.4
Uniform octagonal/square tilings
[8,4], (*842)
(with [8,8] (*882), [(4,4,4)] (*444) , [∞,4,∞] (*4222) index 2 subsymmetries)
(And [(∞,4,∞,4)] (*4242) index 4 subsymmetry)

=

=
=
=
=
=

=

=

=
=


=
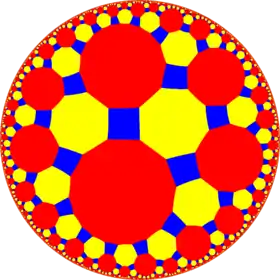{8,4} t{8,4}
 r{8,4} 2t{8,4}=t{4,8} 2r{8,4}={4,8} rr{8,4} tr{8,4}
Uniform duals
V84 V4.16.16 V(4.8)2 V8.8.8 V48 V4.4.4.8 V4.8.16
Alternations
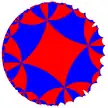
[1+,8,4]
(*444)		 [8+,4]
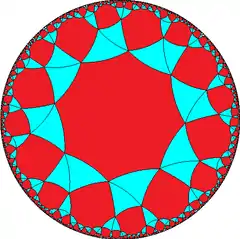
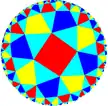
(8*2)		 [8,1+,4]
(*4222)		 [8,4+]
(4*4)		 [8,4,1+]
(*882)		 [(8,4,2+)]
(2*42)		 [8,4]+
(842)

=
=
=
=
=
=
h{8,4} s{8,4} hr{8,4} s{4,8} h{4,8} hrr{8,4} sr{8,4}
Alternation duals
V(4.4)4 V3.(3.8)2 V(4.4.4)2 V(3.4)3 V88 V4.44 V3.3.4.3.8

References

  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

See also

Wikimedia Commons has media related to Uniform tiling 4-4-4-8.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.