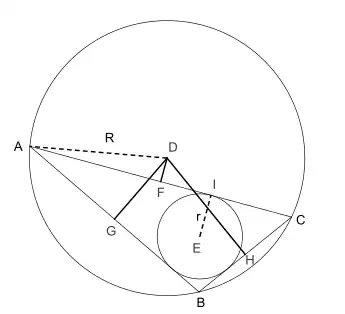
In Euclidean geometry, Carnot's theorem states that the sum of the signed distances from the circumcenter D to the sides of an arbitrary triangle ABC is
where r is the inradius and R is the circumradius of the triangle. Here the sign of the distances is taken to be negative if and only if the open line segment DX (X = F, G, H) lies completely outside the triangle. In the diagram, DF is negative and both DG and DH are positive.
The theorem is named after Lazare Carnot (1753–1823). It is used in a proof of the Japanese theorem for concyclic polygons.
References
- Claudi Alsina, Roger B. Nelsen: When Less is More: Visualizing Basic Inequalities. MAA, 2009, ISBN 978-0-88385-342-9, p.99
- Frédéric Perrier: Carnot's Theorem in Trigonometric Disguise. The Mathematical Gazette, Volume 91, No. 520 (March, 2007), pp. 115–117 (JSTOR)
- David Richeson: The Japanese Theorem for Nonconvex Polygons – Carnot's Theorem. Convergence, December 2013
External links
- Weisstein, Eric W. "Carnot's theorem". MathWorld.
- Carnot's Theorem at cut-the-knot
- Carnot's Theorem by Chris Boucher. The Wolfram Demonstrations Project.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.