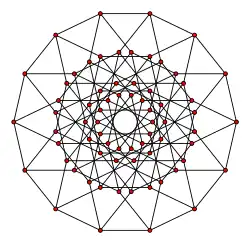
In mathematics, Danzer's configuration is a self-dual configuration of 35 lines and 35 points, having 4 points on each line and 4 lines through each point. It is named after the German geometer Ludwig Danzer and was popularised by Branko Grünbaum.[1] The Levi graph of the configuration is the Kronecker cover of the odd graph O4,[2] and is isomorphic to the middle layer graph of the seven-dimensional hypercube graph Q7. The middle layer graph of an odd-dimensional hypercube graph Q2n+1(n,n+1) is a subgraph whose vertex set consists of all binary strings of length 2n + 1 that have exactly n or n + 1 entries equal to 1, with an edge between any two vertices for which the corresponding binary strings differ in exactly one bit. Every middle layer graph is Hamiltonian.[3]
Danzer's configuration DCD(4) is the fourth term of an infinite series of configurations DCD(n), where DCD(1) is the trivial configuration (11), DCD(2) is the trilateral (32) and DCD(3) is the Desargues configuration (103). In [4] configurations DCD(n) were further generalized to the unbalanced configuration DCD(n,d) by introducing parameter d with connection DCD(n) = DCD(2n-1,n). DCD stands for Desargues-Cayley-Danzer. Each DCD(2n,d) configuration is a subconfiguration of the Clifford configuration. While each DCD(n,d) admits a realisation as a geometric point-line configuration, the Clifford configuration can only be realised as a point-circle configuration and depicts the Clifford's circle theorems.
Example

See also
References
Bibliography
- Boben, Marko; Gévay, Gábor; Pisanski, T. (2015), "Danzer's configuration revisited", Advances in Geometry, 15 (4): 393–408, arXiv:1301.1067, doi:10.1515/advgeom-2015-0019, MR 3406469, S2CID 117048451.
- Gévay, Gábor (2018), "Pascal's triangle of configurations", in Conder, Marston D. E.; Deza, Antoine; Weiss, Asia Ivić (eds.), Discrete Geometry and Symmetry, Springer Proceedings in Mathematics & Statistics, vol. 234, pp. 181–199, doi:10.1007/978-3-319-78434-2_10, ISBN 978-3-319-78433-5, MR 3816877.
- Grünbaum, Branko (2008), "Musing on an example of Danzer's", European Journal of Combinatorics, 29 (8): 1910-1918, doi:10.1016/j.ejc.2008.01.004, MR 2463166.
- Mütze, Torsten (2016), "Proof of the middle levels conjecture" (PDF), Proc. Lond. Math. Soc., 112 (4): 677-713, doi:10.1112/plms/pdw004, MR 3483129, S2CID 119119260.