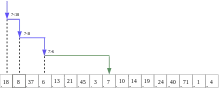
 Visualization of the multiplicative binary search algorithm where 7 is the target value. | |
| Class | Search algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | O(log n) |
| Best-case performance | O(1) |
| Average performance | O(log n) |
| Worst-case space complexity | O(1) |
| Optimal | Yes |
In computer science, multiplicative binary search is a variation of binary search that uses a specific permutation of keys in an array instead of the sorted order used by regular binary search.[1] Multiplicative binary search was first described by Thomas Standish in 1980. This algorithm was originally proposed to simplify the midpoint index calculation on small computers without efficient division or shift operations. On modern hardware, the cache-friendly nature of multiplicative binary search makes it suitable for out-of-core search on block-oriented storage as an alternative to B-trees and B+ trees. For optimal performance, the branching factor of a B-tree or B+-tree must match the block size of the file system that it is stored on. The permutation used by multiplicative binary search places the optimal number of keys in the first (root) block, regardless of block size.
Multiplicative binary search is used by some optimizing compilers to implement switch statements.[2][3]
Algorithm
Multiplicative binary search operates on a permuted sorted array. Keys are stored in the array in level-order sequence of the corresponding balanced binary search tree. This places the first pivot of a binary search as the first element in the array. The second pivots are placed at the next two positions.
Given an array A of n elements with values A0 ... An−1, and target value T, the following subroutine uses multiplicative binary search to find the index of T in A.
- Set i to 0
- if i ≥ n, the search terminates unsuccessful.
- if Ai = T, the search is done; return i.
- if Ai < T, set i to 2×i + 1 and go to step 2.
- if Ai > T, set i to 2×i + 2 and go to step 2.
See also
- Binary search tree – Rooted binary tree data structure
- Methods for storing binary trees – Limited form of tree data structure
- Ahnentafel – Genealogical numbering system for listing a person's direct ancestors
Citations
- ↑ Standish, Thomas A. (1980). "Chapter 4.2.2: Ordered Table Search". Data Structure Techniques. Addison-Wesley. pp. 136–141. ISBN 978-0201072563.
- ↑ Sayle, Roger A. (17 June 2008). "A Superoptimizer Analysis of Multiway Branch Code Generation" (PDF). Proceedings of the GCC Developers' Summit: 103–116. Retrieved 4 March 2017.
- ↑ Spuler, David A. (January 1994). Compiler Code Generation for Multiway Branch Statements as a Static Search Problem (Technical report). Department of Computer Science, James Cook University, Australia. 94/03.