The Fibonacci word fractal is a fractal curve defined on the plane from the Fibonacci word.

Definition

The first iterations

L-system representation^[1]

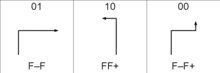
This curve is built iteratively by applying the Odd–Even Drawing rule to the Fibonacci word 0100101001001...:

For each digit at position k:

1. Draw a segment forward
2. If the digit is 0:
   • Turn 90° to the left if k is even
   • Turn 90° to the right if k is odd

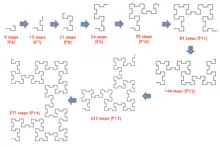
To a Fibonacci word of length ${\displaystyle F_{n}}$ (the n^th Fibonacci number) is associated a curve ${\displaystyle {\mathcal {F}}_{n}}$ made of ${\displaystyle F_{n}}$ segments. The curve displays three different aspects whether n is in the form 3k, 3k + 1, or 3k + 2.

Properties

The Fibonacci numbers in the Fibonacci word fractal.

Some of the Fibonacci word fractal's properties include:^[2][3]

• The curve ${\displaystyle {\mathcal {F_{n}}}}$ contains ${\displaystyle F_{n}}$ segments, ${\displaystyle F_{n-1}}$ right angles and ${\displaystyle F_{n-2}}$ flat angles.
• The curve never self-intersects and does not contain double points. At the limit, it contains an infinity of points asymptotically close.
• The curve presents self-similarities at all scales. The reduction ratio is ${\displaystyle 1+{\sqrt {2}}}$. This number, also called the silver ratio, is present in a great number of properties listed below.
• The number of self-similarities at level n is a Fibonacci number \ −1. (more precisely: ${\displaystyle F_{3n+3}-1}$).
• The curve encloses an infinity of square structures of decreasing sizes in a ratio ${\displaystyle 1+{\sqrt {2}}}$ (see figure). The number of those square structures is a Fibonacci number.
• The curve ${\displaystyle {\mathcal {F}}_{n}}$can also be constructed in different ways (see gallery below):
  • Iterated function system of 4 and 1 homothety of ratio ${\displaystyle 1/(1+{\sqrt {2}})}$ and ${\displaystyle 1/(1+{\sqrt {2}})^{2}}$
  • By joining together the curves ${\displaystyle {\mathcal {F}}_{n-1}}$ and ${\displaystyle {\mathcal {F}}_{n-2}}$
  • Lindenmayer system
  • By an iterated construction of 8 square patterns around each square pattern.
  • By an iterated construction of octagons
• The Hausdorff dimension of the Fibonacci word fractal is ${\displaystyle 3\,{\frac {\log \varphi }{\log(1+{\sqrt {2}})}}\approx 1.6379}$, with ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ the golden ratio.
• Generalizing to an angle ${\displaystyle \alpha }$ between 0 and ${\displaystyle \pi /2}$, its Hausdorff dimension is ${\displaystyle 3\,{\frac {\log \varphi }{\log(1+a+{\sqrt {(1+a)^{2}+1}})}}}$, with ${\displaystyle a=\cos \alpha }$.
• The Hausdorff dimension of its frontier is ${\displaystyle {\frac {\log 3}{{\log(1+{\sqrt {2}}})}}\approx 1.2465}$.
• Exchanging the roles of "0" and "1" in the Fibonacci word, or in the drawing rule yields a similar curve, but oriented 45°.
• From the Fibonacci word, one can define the «dense Fibonacci word», on an alphabet of 3 letters: 102210221102110211022102211021102110221022102211021... (sequence A143667 in the OEIS). The usage, on this word, of a more simple drawing rule, defines an infinite set of variants of the curve, among which:
  • a "diagonal variant"
  • a "svastika variant"
  • a "compact variant"
• It is conjectured that the Fibonacci word fractal appears for every sturmian word for which the slope, written in continued fraction expansion, ends with an infinite sequence of "1"s.

Gallery

• 
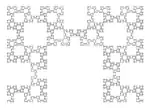  Curve after ${\displaystyle \textstyle {F_{23}}}$ iterations.
• 
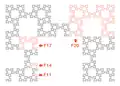  Self-similarities at different scales.
• 
  Dimensions.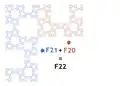
• 
  Construction by juxtaposition (1)
• 
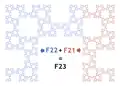  Construction by juxtaposition (2)
• 
  Order 18, with some sub-rectangles colored.
• 
• 
  Construction by iterated suppression of square patterns.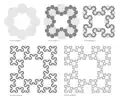
• 
  Construction by iterated octagons.
• 
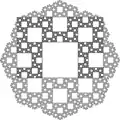  Construction by iterated collection of 8 square patterns around each square pattern.
• 
  With a 60° angle.
• 
  Inversion of "0" and "1".
• 
  Variants generated from the dense Fibonacci word.
• 
  The "compact variant"
• 
  The "svastika variant"
• 
  The "diagonal variant"
• 
  The "π/8 variant"
• 
  Artist creation (Samuel Monnier).

The Fibonacci tile

Imperfect tiling by the Fibonacci tile. The area of the central square tends to infinity.

The juxtaposition of four ${\displaystyle F_{3k}}$ curves allows the construction of a closed curve enclosing a surface whose area is not null. This curve is called a "Fibonacci tile".

• The Fibonacci tile almost tiles the plane. The juxtaposition of 4 tiles (see illustration) leaves at the center a free square whose area tends to zero as k tends to infinity. At the limit, the infinite Fibonacci tile tiles the plane.
• If the tile is enclosed in a square of side 1, then its area tends to ${\displaystyle 2-{\sqrt {2}}=0.5857}$.

Perfect tiling by the Fibonacci snowflake

Fibonacci snowflake

Fibonacci snowflakes for i = 2 for n = 1 through 4: ${\displaystyle \sideset {}{_{1}^{\left[2\right]}\quad }\prod }$, ${\displaystyle \sideset {}{_{2}^{\left[2\right]}\quad }\prod }$, ${\displaystyle \sideset {}{_{3}^{\left[2\right]}\quad }\prod }$, ${\displaystyle \sideset {}{_{4}^{\left[2\right]}\quad }\prod }$^[4]

The Fibonacci snowflake is a Fibonacci tile defined by:^[5]

• ${\displaystyle q_{n}=q_{n-1}q_{n-2}}$ if ${\displaystyle n\equiv 2{\pmod {3}}}$
• ${\displaystyle q_{n}=q_{n-1}{\overline {q}}_{n-2}}$ otherwise.

with ${\displaystyle q_{0}=\epsilon }$ and ${\displaystyle q_{1}=R}$, ${\displaystyle L=}$ "turn left" and ${\displaystyle R=}$ "turn right", and ${\displaystyle {\overline {R}}=L}$.

Several remarkable properties:^[5][6]

• It is the Fibonacci tile associated to the "diagonal variant" previously defined.
• It tiles the plane at any order.
• It tiles the plane by translation in two different ways.
• its perimeter at order n equals ${\displaystyle 4F(3n+1)}$, where ${\displaystyle F(n)}$ is the n^th Fibonacci number.
• its area at order n follows the successive indexes of odd row of the Pell sequence (defined by ${\displaystyle P(n)=2P(n-1)+P(n-2)}$).

See also

• Golden ratio
• Fibonacci number
• Fibonacci word
• List of fractals by Hausdorff dimension

References

External links

• "Generate a Fibonacci word fractal", OnlineMathTools.com.