The hour angle is indicated by an orange arrow on the celestial equator plane. The arrow ends at the hour circle of an orange dot indicating the apparent place of an astronomical object on the celestial sphere.

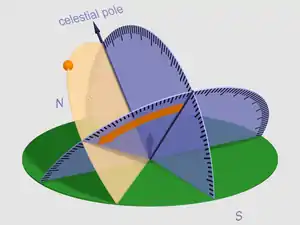
In astronomy and celestial navigation, the hour angle is the dihedral angle between the meridian plane (containing Earth's axis and the zenith) and the hour circle (containing Earth's axis and a given point of interest).^[1]

It may be given in degrees, time, or rotations depending on the application. The angle may be expressed as negative east of the meridian plane and positive west of the meridian plane, or as positive westward from 0° to 360°. The angle may be measured in degrees or in time, with 24^h = 360° exactly. In celestial navigation, the convention is to measure in degrees westward from the prime meridian (Greenwich hour angle, GHA), from the local meridian (local hour angle, LHA) or from the first point of Aries (sidereal hour angle, SHA).

The hour angle is paired with the declination to fully specify the location of a point on the celestial sphere in the equatorial coordinate system.^[2]

Relation with right ascension

As seen from above the Earth's north pole, a star's local hour angle (LHA) for an observer near New York (red dot). Also depicted are the star's right ascension and Greenwich hour angle (GHA), the local mean sidereal time (LMST) and Greenwich mean sidereal time (GMST). The symbol ʏ identifies the vernal equinox direction.
Assuming in this example the day of the year is the March equinox so the sun lies in the direction of the grey arrow then this star will rise about midnight. Just after the observer reaches the green arrow dawn comes and overwhelms with light the visibility of the star about six hours before it sets on the western horizon. The Right Ascension of the star is about 18^h

The local hour angle (LHA) of an object in the observer's sky is

$${\displaystyle {\text{LHA}}_{\text{object}}={\text{LST}}-\alpha _{\text{object}}}$$

or

$${\displaystyle {\text{LHA}}_{\text{object}}={\text{GST}}+\lambda _{\text{observer}}-\alpha _{\text{object}}}$$

where LHA_object is the local hour angle of the object, LST is the local sidereal time, ${\displaystyle \alpha _{\text{object}}}$ is the object's right ascension, GST is Greenwich sidereal time and ${\displaystyle \lambda _{\text{observer}}}$ is the observer's longitude (positive east from the prime meridian).^[3] These angles can be measured in time (24 hours to a circle) or in degrees (360 degrees to a circle)—one or the other, not both.

Negative hour angles (−180° < LHA_object < 0°) indicate the object is approaching the meridian, positive hour angles (0° < LHA_object < 180°) indicate the object is moving away from the meridian; an hour angle of zero means the object is on the meridian.

Solar hour angle

Observing the Sun from Earth, the solar hour angle is an expression of time, expressed in angular measurement, usually degrees, from solar noon. At solar noon the hour angle is zero degrees, with the time before solar noon expressed as negative degrees, and the local time after solar noon expressed as positive degrees. For example, at 10:30 AM local apparent time the hour angle is −22.5° (15° per hour times 1.5 hours before noon).^[4]

The cosine of the hour angle (cos(h)) is used to calculate the solar zenith angle. At solar noon, h = 0.000 so cos(h) = 1, and before and after solar noon the cos(± h) term = the same value for morning (negative hour angle) or afternoon (positive hour angle), so that the Sun is at the same altitude in the sky at 11:00AM and 1:00PM solar time.^[5]

Sidereal hour angle

The sidereal hour angle (SHA) of a body on the celestial sphere is its angular distance west of the vernal equinox generally measured in degrees. The SHA of a star varies by less than a minute of arc per year, due to precession, while the SHA of a planet varies significantly from night to night. SHA is often used in celestial navigation and navigational astronomy, and values are published in astronomical almanacs.

See also

• Clock position
• List of orbits

Notes and references