

Hoffman's packing puzzle is an assembly puzzle named after Dean G. Hoffman, who described it in 1978.[1] The puzzle consists of 27 identical rectangular cuboids, each of whose edges have three different lengths. Its goal is to assemble them all to fit within a cube whose edge length is the sum of the three lengths.[2][3]
Hoffman (1981) writes that the first person to solve the puzzle was David A. Klarner, and that typical solution times can range from 20 minutes to multiple hours.[2]
Construction
The puzzle itself consists only of 27 identical rectangular cuboid-shaped blocks, although physical realizations of the puzzle also typically supply a cubical box to fit the blocks into. If the three lengths of the block edges are x, y, and z, then the cube should have edge length x + y + z. Although the puzzle can be constructed with any three different edge lengths, it is most difficult when the three edge lengths of the blocks are close enough together that x + y + z < 4 min(x,y,z), as this prevents alternative solutions in which four blocks of the minimum width are packed next to each other. Additionally, having the three lengths form an arithmetic progression can make it more confusing, because in this case placing three blocks of the middle width next to each other produces a row of the correct total width but one that cannot lead to a valid solution to the whole puzzle.[2]
Mathematical analysis
Each valid solution to the puzzle arranges the blocks in an approximate 3 × 3 × 3 grid of blocks, with the sides of the blocks all parallel to the sides of the outer cube, and with one block of each width along each axis-parallel line of three blocks. Counting reflections and rotations as being the same solution as each other, the puzzle has 21 combinatorially distinct solutions.[2][4]
The total volume of the pieces, 27xyz, is less than the volume (x + y + z)3 of the cube that they pack into. If one takes the cube root of both volumes, and divides by three, then the number obtained in this way from the total volume of the pieces is the geometric mean of x, y, and z, while the number obtained in the same way from the volume of the cube is their arithmetic mean. The fact that the pieces have less total volume than the cube follows from the inequality of arithmetic and geometric means.[2][3]
Table of solutions
The 21 distinct solutions are tabulated here as described by the references cited above [2][4].
All boxes below are entered in the format (east-west length) x (north-south length) x (up-down length), denoting the size of each box with the dimensions A, B, and C, where A < B < C. (In the above example, A = 4, B = 5, and C = 6).
All 3x3 matrices describe a set of 9 boxes, with east-west neighbors along each row and north-south neighbors down each column, with the three stacked layers being listed in sequence for each solution.
| Solution | Bottom layer | Middle layer | Top layer |
|---|---|---|---|
| Solution 01 | CxBxA AxCxB BxAxC BxCxA CxAxB AxBxC AxCxB BxAxC CxBxA |
CxAxB AxBxC BxCxA AxBxC BxAxC AxCxB BxCxA CxBxA CxAxB |
BxAxC CxBxA AxCxB CxAxB BxCxA CxBxA AxBxC AxCxB BxAxC |
| Solution 02 | CxBxA AxCxB BxAxC BxCxA CxAxB AxBxC AxCxB BxAxC CxBxA |
CxAxB AxBxC AxCxB AxBxC BxAxC BxCxA BxCxA CxBxA CxAxB |
BxAxC BxCxA CxBxA CxAxB CxBxA AxCxB AxBxC AxCxB BxAxC |
| Solution 03 | CxBxA AxCxB BxAxC BxCxA CxAxB AxBxC AxCxB BxAxC CxBxA |
AxBxC BxAxC BxCxA CxAxB AxBxC AxCxB BxCxA CxBxA CxAxB |
CxAxB CxBxA AxCxB BxAxC BxCxA CxBxA AxBxC AxCxB BxAxC |
| Solution 04 | CxBxA AxCxB BxAxC BxCxA CxAxB AxBxC AxCxB BxAxC CxBxA |
AxBxC BxAxC AxCxB CxAxB AxBxC BxCxA BxCxA CxBxA CxAxB |
CxAxB BxCxA CxBxA BxAxC CxBxA AxCxB AxBxC AxCxB BxAxC |
| Solution 05 | CxBxA AxCxB CxAxB BxCxA CxBxA BxAxC AxCxB BxAxC AxBxC |
AxBxC BxCxA BxAxC BxAxC AxCxB CxBxA CxBxA CxAxB AxCxB |
AxCxB BxAxC CxBxA CxAxB AxBxC AxCxB BxAxC CxBxA BxCxA |
| Solution 06 | CxBxA AxCxB CxAxB BxCxA CxBxA BxAxC AxCxB BxAxC AxBxC |
AxBxC BxCxA BxAxC CxAxB AxCxB CxBxA BxAxC CxBxA AxCxB |
AxCxB BxAxC CxBxA BxAxC AxBxC AxCxB CxBxA CxAxB BxCxA |
| Solution 07 | CxBxA AxCxB BxAxC BxCxA CxBxA CxAxB AxCxB BxAxC AxBxC |
CxAxB CxBxA BxCxA BxAxC AxCxB AxBxC AxBxC BxCxA CxAxB |
AxBxC BxAxC AxCxB CxAxB AxBxC BxCxA BxCxA CxAxB CxBxA |
| Solution 08 | CxBxA AxCxB BxAxC BxCxA CxBxA CxAxB AxCxB BxAxC AxBxC |
BxAxC CxBxA BxCxA CxAxB AxCxB AxBxC AxBxC BxCxA CxAxB |
CxAxB AxBxC AxCxB AxBxC BxAxC BxCxA BxCxA CxAxB CxBxA |
| Solution 09 | CxBxA AxCxB BxAxC BxCxA CxBxA CxAxB AxCxB BxAxC AxBxC |
AxBxC BxCxA CxAxB BxAxC AxCxB AxBxC CxBxA CxAxB BxCxA |
AxCxB BxAxC CxBxA CxAxB AxBxC BxCxA BxAxC CxBxA AxCxB |
| Solution 10 | CxBxA AxCxB BxAxC BxCxA CxBxA CxAxB AxCxB BxAxC AxBxC |
AxBxC BxCxA CxAxB CxAxB AxCxB AxBxC BxAxC CxBxA BxCxA |
AxCxB BxAxC CxBxA BxAxC AxBxC BxCxA CxBxA CxAxB AxCxB |
| Solution 11 | CxBxA AxCxB BxAxC BxCxA BxAxC AxBxC AxCxB CxBxA CxAxB |
CxAxB AxBxC BxCxA AxBxC CxAxB AxCxB BxCxA BxAxC CxBxA |
BxAxC CxBxA AxCxB CxAxB BxCxA CxBxA AxBxC AxCxB BxAxC |
| Solution 12 | CxBxA AxCxB BxAxC BxCxA BxAxC AxBxC AxCxB CxBxA CxAxB |
CxAxB AxBxC AxCxB AxBxC CxAxB BxCxA BxCxA BxAxC CxBxA |
BxAxC BxCxA CxBxA CxAxB CxBxA AxCxB AxBxC AxCxB BxAxC |
| Solution 13 | CxBxA AxCxB BxAxC BxCxA BxAxC AxBxC AxCxB CxAxB CxBxA |
CxAxB AxBxC AxCxB AxBxC BxCxA CxAxB BxCxA CxBxA BxAxC |
BxAxC CxBxA BxCxA CxAxB AxCxB CxBxA AxBxC BxAxC AxCxB |
| Solution 14 | CxBxA AxCxB BxAxC BxCxA BxAxC AxBxC AxCxB CxAxB CxBxA |
BxAxC AxBxC AxCxB AxCxB CxBxA CxAxB CxBxA BxCxA BxAxC |
CxAxB CxBxA BxCxA BxAxC AxCxB CxBxA AxBxC BxAxC AxCxB |
| Solution 15 | CxBxA BxCxA CxAxB BxCxA CxAxB AxBxC AxCxB AxBxC BxAxC |
CxAxB AxBxC BxCxA AxBxC BxAxC AxCxB BxCxA CxBxA CxAxB |
BxAxC AxCxB AxBxC CxAxB BxCxA CxBxA AxBxC CxAxB BxCxA |
| Solution 16 | CxBxA BxCxA CxAxB BxCxA CxAxB AxBxC AxCxB AxBxC BxAxC |
CxAxB AxBxC BxCxA AxBxC BxAxC AxCxB BxCxA CxAxB CxBxA |
BxAxC AxCxB AxBxC CxAxB CxBxA BxCxA AxBxC BxCxA CxAxB |
| Solution 17 | CxBxA BxCxA CxAxB BxCxA CxAxB AxBxC AxCxB AxBxC BxAxC |
CxAxB AxCxB AxBxC AxBxC BxAxC BxCxA BxCxA CxAxB CxBxA |
BxAxC AxBxC BxCxA CxAxB CxBxA AxCxB AxBxC BxCxA CxAxB |
| Solution 18 | CxBxA BxCxA CxAxB BxCxA CxAxB AxBxC AxCxB AxBxC BxAxC |
BxAxC AxCxB AxBxC CxAxB BxCxA CxBxA AxBxC CxAxB BxCxA |
CxAxB AxBxC BxCxA AxBxC BxAxC AxCxB BxCxA CxBxA CxAxB |
| Solution 19 | CxBxA BxCxA CxAxB BxCxA CxAxB AxBxC AxCxB AxBxC BxAxC |
AxCxB BxAxC CxBxA BxAxC AxBxC BxCxA CxBxA CxAxB AxCxB |
AxBxC AxCxB BxAxC CxAxB CxBxA AxCxB BxAxC BxCxA CxBxA |
| Solution 20 | CxBxA BxCxA CxAxB BxCxA CxAxB AxBxC AxCxB AxBxC BxAxC |
AxCxB BxAxC CxBxA BxAxC AxBxC AxCxB CxBxA CxAxB BxCxA |
AxBxC AxCxB BxAxC CxAxB BxCxA CxBxA BxAxC CxBxA AxCxB |
| Solution 21 | CxBxA BxCxA CxAxB BxCxA CxAxB AxBxC AxCxB AxBxC BxAxC |
AxBxC AxCxB BxAxC BxAxC BxCxA CxBxA CxBxA CxAxB AxCxB |
AxCxB BxAxC CxBxA CxAxB AxBxC AxCxB BxAxC CxBxA BxCxA |
Higher dimensions
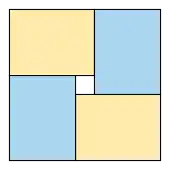
A two-dimensional analogue of the puzzle asks to pack four identical rectangles of side lengths x and y into a square of side length x + y; as the figure shows, this is always possible. In d dimensions the puzzle asks to pack dd identical blocks into a hypercube. By a result of Raphael M. Robinson this is again solvable whenever d = d1 × d2 for two numbers d1 and d2 such that the d1- and d2-dimensional cases are themselves solvable. For instance, according to this result, it is solvable for dimensions 4, 6, 8, 9, and other 3-smooth numbers. In all dimensions, the inequality of arithmetic and geometric means shows that the volume of the pieces is less than the volume of the hypercube into which they should be packed. However, it is unknown whether the puzzle can be solved in five dimensions, or in higher prime number dimensions.[2][5]
References
- ↑ Rausch, John, "Put-Together – Hoffman's Packing Puzzle", Puzzle World, archived from the original on 2019-11-17, retrieved 2019-11-16
- 1 2 3 4 5 6 7 Hoffman, D. G. (1981), "Packing problems and inequalities", in Klarner, David A. (ed.), The Mathematical Gardner, Springer, pp. 212–225, doi:10.1007/978-1-4684-6686-7_19
- 1 2 Alsina, Claudi; Nelsen, Roger B. (2015), "Problem 3.10", A Mathematical Space Odyssey: Solid Geometry in the 21st Century, Dolciani Mathematical Expositions, vol. 50, Mathematical Association of America, p. 63, ISBN 9780883853580
- 1 2 Berlekamp, Elwyn R.; Conway, John H.; Guy, Richard K. (2004), Winning Ways for Your Mathematical Plays, vol. IV, A K Peters, pp. 913–915
- ↑ von Holck, Nikolaj Ingemann (January 2018), An Experimental Approach to Packing Problems (PDF), Bachelor's thesis, supervised by Søren Eilers, University of Copenhagen, archived (PDF) from the original on 2019-11-17, retrieved 2019-11-17