Uniform honeycombs in hyperbolic space

Unsolved problem in mathematics:

Find the complete set of hyperbolic uniform honeycombs.

In hyperbolic geometry, a uniform honeycomb in hyperbolic space is a uniform tessellation of uniform polyhedral cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by permutations of rings of the Coxeter diagrams for each family.

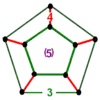
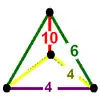
Four compact regular hyperbolic honeycombs
Poincaré ball model projections
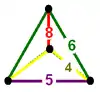
Order-4 dodecahedral honeycomb ${5,3,4}$	Order-5 dodecahedral honeycomb ${5,3,5}$
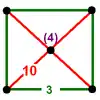
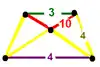
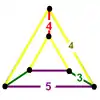
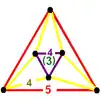
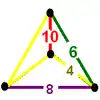
Order-5 cubic honeycomb ${4,3,5}$	Icosahedral honeycomb ${3,5,3}$

Hyperbolic uniform honeycomb families

Honeycombs are divided between compact and paracompact forms defined by Coxeter groups, the first category only including finite cells and vertex figures (finite subgroups), and the second includes affine subgroups.

Compact uniform honeycomb families

The nine compact Coxeter groups are listed here with their Coxeter diagrams,^[1] in order of the relative volumes of their fundamental simplex domains.^[2]

These 9 families generate a total of 76 unique uniform honeycombs. The full list of hyperbolic uniform honeycombs has not been proven and an unknown number of non-Wythoffian forms exist. Two known examples are cited with the {3,5,3} family below. Only two families are related as a mirror-removal halving: [5,3^1,1] ↔ [5,3,4,1⁺].

Indexed	Fundamental simplex volume^[3]	Witt symbol	Coxeter notation	Commutator subgroup	Honeycombs
H₁	0.0358850633	${\bar {BH}}_{3}$	[5,3,4]	[(5,3)⁺,4,1⁺] = [5,3^1,1]⁺	15 forms, 2 regular
H₂	0.0390502856	${\bar {J}}_{3}$	[3,5,3]	[3,5,3]⁺	9 forms, 1 regular
H₃	0.0717701267	${\bar {DH}}_{3}$	[5,3^1,1]	[5,3^1,1]⁺	11 forms (7 overlap with [5,3,4] family, 4 are unique)
H₄	0.0857701820	${\widehat {AB}}_{3}$	[(4,3,3,3)]	[(4,3,3,3)]⁺	9 forms
H₅	0.0933255395	${\bar {K}}_{3}$	[5,3,5]	[5,3,5]⁺	9 forms, 1 regular
H₆	0.2052887885	${\widehat {AH}}_{3}$	[(5,3,3,3)]	[(5,3,3,3)]⁺	9 forms
H₇	0.2222287320	${\widehat {BB}}_{3}$	[(4,3)^[2]]	[(4,3⁺,4,3⁺)]	6 forms
H₈	0.3586534401	${\widehat {BH}}_{3}$	[(3,4,3,5)]	[(3,4,3,5)]⁺	9 forms
H₉	0.5021308905	${\widehat {HH}}_{3}$	[(5,3)^[2]]	[(5,3)^[2]]⁺	6 forms

There are just two radical subgroups with non-simplicial domains that can be generated by removing a set of two or more mirrors separated by all other mirrors by even-order branches. One is [(4,3,4,3^*)], represented by Coxeter diagrams an index 6 subgroup with a trigonal trapezohedron fundamental domain ↔ , which can be extended by restoring one mirror as . The other is [4,(3,5)^*], index 120 with a dodecahedral fundamental domain.

Paracompact hyperbolic uniform honeycombs

There are also 23 paracompact Coxeter groups of rank 4 that produce paracompact uniform honeycombs with infinite or unbounded facets or vertex figure, including ideal vertices at infinity.

Hyperbolic paracompact group summary
Type	Coxeter groups
Linear graphs	\| \| \| \| \|
Tridental graphs	\|
Cyclic graphs	\| \| \| \| \| \| \|
Loop-n-tail graphs	\| \|

Other paracompact Coxeter groups exists as Vinberg polytope fundamental domains, including these triangular bipyramid fundamental domains (double tetrahedra) as rank 5 graphs including parallel mirrors. Uniform honeycombs exist as all permutations of rings in these graphs, with the constraint that at least one node must be ringed across infinite order branches.

Dimension	Rank	Graphs
H³	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

[3,5,3] family

There are 9 forms, generated by ring permutations of the Coxeter group: [3,5,3] or

One related non-wythoffian form is constructed from the {3,5,3} vertex figure with 4 (tetrahedrally arranged) vertices removed, creating pentagonal antiprisms and dodecahedra filling in the gaps, called a tetrahedrally diminished dodecahedron.^[4] Another is constructed with 2 antipodal vertices removed.^[5]

The bitruncated and runcinated forms (5 and 6) contain the faces of two regular skew polyhedrons: {4,10|3} and {10,4|3}.

#	Honeycomb name Coxeter diagram and Schläfli symbols	Cell counts/vertex and positions in honeycomb				Vertex figure	Picture
#	Honeycomb name Coxeter diagram and Schläfli symbols	0	1	2	3	Vertex figure	Picture
1	icosahedral (ikhon) t₀{3,5,3}				(12) (3.3.3.3.3)
2	rectified icosahedral (rih) t₁{3,5,3}	(2) (5.5.5)			(3) (3.5.3.5)
3	truncated icosahedral (tih) t_0,1{3,5,3}	(1) (5.5.5)			(3) (5.6.6)
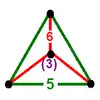4	cantellated icosahedral (srih) t_0,2{3,5,3}	(1) (3.5.3.5)	(2) (4.4.3)		(2) (3.5.4.5)
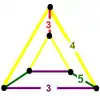5	runcinated icosahedral (spiddih) t_0,3{3,5,3}	(1) (3.3.3.3.3)	(5) (4.4.3)	(5) (4.4.3)	(1) (3.3.3.3.3)
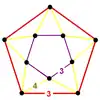6	bitruncated icosahedral (dih) t_1,2{3,5,3}	(2) (3.10.10)			(2) (3.10.10)
7	cantitruncated icosahedral (grih) t_0,1,2{3,5,3}	(1) (3.10.10)	(1) (4.4.3)		(2) (4.6.10)
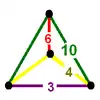8	runcitruncated icosahedral (prih) t_0,1,3{3,5,3}	(1) (3.5.4.5)	(1) (4.4.3)	(2) (4.4.6)	(1) (5.6.6)
9	omnitruncated icosahedral (gipiddih) t_0,1,2,3{3,5,3}	(1) (4.6.10)	(1) (4.4.6)	(1) (4.4.6)	(1) (4.6.10)

#	Honeycomb name Coxeter diagram and Schläfli symbols	Cell counts/vertex and positions in honeycomb					Vertex figure	Picture
#	Honeycomb name Coxeter diagram and Schläfli symbols	0	1	2	3	Alt	Vertex figure	Picture
[77]	partially diminished icosahedral pd{3,5,3}^[6]				(12) (3.3.3.5)	(4) (5.5.5)
[78]	semi-partially diminished icosahedral spd{3,5,3}^[5]				(6) (3.3.3.5) (6) (3.3.3.3.3)	(2) (5.5.5)
Nonuniform	omnisnub icosahedral (snih) ht_0,1,2,3{3,5,3}	(1) (3.3.3.3.5)	(1) (3.3.3.3	(1) (3.3.3.3)	(1) (3.3.3.3.5)	(4) +(3.3.3)

[5,3,4] family

There are 15 forms, generated by ring permutations of the Coxeter group: [5,3,4] or .

This family is related to the group [5,3^1,1] by a half symmetry [5,3,4,1⁺], or ↔ , when the last mirror after the order-4 branch is inactive, or as an alternation if the third mirror is inactive ↔ .

#	Name of honeycomb Coxeter diagram	Cells by location and count per vertex				Vertex figure	Picture
#	Name of honeycomb Coxeter diagram	0	1	2	3	Vertex figure	Picture
10	order-4 dodecahedral (doehon) ↔	-	-	-	(8) (5.5.5)
11	rectified order-4 dodecahedral (riddoh) ↔	(2) (3.3.3.3)	-	-	(4) (3.5.3.5)
12	rectified order-5 cubic (ripech) ↔	(5) (3.4.3.4)	-	-	(2) (3.3.3.3.3)
13	order-5 cubic (pechon)	(20) (4.4.4)	-	-	-
14	truncated order-4 dodecahedral (tiddoh) ↔	(1) (3.3.3.3)	-	-	(4) (3.10.10)
15	bitruncated order-5 cubic (ciddoh) ↔	(2) (4.6.6)	-	-	(2) (5.6.6)
16	truncated order-5 cubic (tipech)	(5) (3.8.8)	-	-	(1) (3.3.3.3.3)
17	cantellated order-4 dodecahedral (sriddoh) ↔	(1) (3.4.3.4)	(2) (4.4.4)	-	(2) (3.4.5.4)
18	cantellated order-5 cubic (sripech)	(2) (3.4.4.4)	-	(2) (4.4.5)	(1) (3.5.3.5)
19	runcinated order-5 cubic (sidpicdoh)	(1) (4.4.4)	(3) (4.4.4)	(3) (4.4.5)	(1) (5.5.5)
20	cantitruncated order-4 dodecahedral (griddoh) ↔	(1) (4.6.6)	(1) (4.4.4)	-	(2) (4.6.10)
21	cantitruncated order-5 cubic (gripech)	(2) (4.6.8)	-	(1) (4.4.5)	(1) (5.6.6)
22	runcitruncated order-4 dodecahedral (pripech)	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.10)	(1) (3.10.10)
23	runcitruncated order-5 cubic (priddoh)	(1) (3.8.8)	(2) (4.4.8)	(1) (4.4.5)	(1) (3.4.5.4)
24	omnitruncated order-5 cubic (gidpicdoh)	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.10)	(1) (4.6.10)

#	Name of honeycomb Coxeter diagram	Cells by location and count per vertex					Vertex figure	Picture
#	Name of honeycomb Coxeter diagram	0	1	2	3	Alt	Vertex figure	Picture
[34]	alternated order-5 cubic (apech) ↔	(20) (3.3.3)			(12) (3.3.3.3.3)
[35]	cantic order-5 cubic (tapech) ↔	(1) (3.5.3.5)	-	(2) (5.6.6)	(2) (3.6.6)
[36]	runcic order-5 cubic (birapech) ↔	(1) (5.5.5)	-	(3) (3.4.5.4)	(1) (3.3.3)
[37]	runcicantic order-5 cubic (bitapech) ↔	(1) (3.10.10)	-	(2) (4.6.10)	(1) (3.6.6)
Nonuniform	snub rectified order-4 dodecahedral	(1) (3.3.3.3.3)	(1) (3.3.3)	-	(2) (3.3.3.3.5)	(4) +(3.3.3)	Irr. tridiminished icosahedron
Nonuniform	runcic snub rectified order-4 dodecahedral	(3.4.4.4)	(4.4.4.4)	-	(3.3.3.3.5)	+(3.3.3)
Nonuniform	omnisnub order-5 cubic	(1) (3.3.3.3.4)	(1) (3.3.3.4)	(1) (3.3.3.5)	(1) (3.3.3.3.5)	(4) +(3.3.3)

[5,3,5] family

There are 9 forms, generated by ring permutations of the Coxeter group: [5,3,5] or

The bitruncated and runcinated forms (29 and 30) contain the faces of two regular skew polyhedrons: {4,6|5} and {6,4|5}.

#	Name of honeycomb Coxeter diagram	Cells by location and count per vertex				Vertex figure	Picture
#	Name of honeycomb Coxeter diagram	0	1	2	3	Vertex figure	Picture
25	(Regular) Order-5 dodecahedral (pedhon) t₀{5,3,5}				(20) (5.5.5)
26	rectified order-5 dodecahedral (ripped) t₁{5,3,5}	(2) (3.3.3.3.3)			(5) (3.5.3.5)
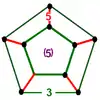27	truncated order-5 dodecahedral (tipped) t_0,1{5,3,5}	(1) (3.3.3.3.3)			(5) (3.10.10)
28	cantellated order-5 dodecahedral (sripped) t_0,2{5,3,5}	(1) (3.5.3.5)	(2) (4.4.5)		(2) (3.5.4.5)
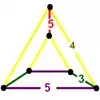29	Runcinated order-5 dodecahedral (spidded) t_0,3{5,3,5}	(1) (5.5.5)	(3) (4.4.5)	(3) (4.4.5)	(1) (5.5.5)
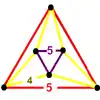30	bitruncated order-5 dodecahedral (diddoh) t_1,2{5,3,5}	(2) (5.6.6)			(2) (5.6.6)
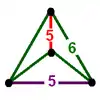31	cantitruncated order-5 dodecahedral (gripped) t_0,1,2{5,3,5}	(1) (5.6.6)	(1) (4.4.5)		(2) (4.6.10)
32	runcitruncated order-5 dodecahedral (pripped) t_0,1,3{5,3,5}	(1) (3.5.4.5)	(1) (4.4.5)	(2) (4.4.10)	(1) (3.10.10)
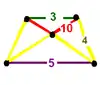33	omnitruncated order-5 dodecahedral (gipidded) t_0,1,2,3{5,3,5}	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.10)	(1) (4.6.10)

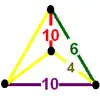#	Name of honeycomb Coxeter diagram	Cells by location and count per vertex					Vertex figure	Picture
#	Name of honeycomb Coxeter diagram	0	1	2	3	Alt	Vertex figure	Picture
Nonuniform	omnisnub order-5 dodecahedral ht_0,1,2,3{5,3,5}	(1) (3.3.3.3.5)	(1) (3.3.3.5)	(1) (3.3.3.5)	(1) (3.3.3.3.5)	(4) +(3.3.3)

[5,3^1,1] family

There are 11 forms (and only 4 not shared with [5,3,4] family), generated by ring permutations of the Coxeter group: [5,3^1,1] or . If the branch ring states match, an extended symmetry can double into the [5,3,4] family, ↔ .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				vertex figure	Picture
#	Honeycomb name Coxeter diagram	0	1	0'	3	vertex figure	Picture
34	alternated order-5 cubic (apech) ↔	-	-	(12) (3.3.3.3.3)	(20) (3.3.3)
35	cantic order-5 cubic (tapech) ↔	(1) (3.5.3.5)	-	(2) (5.6.6)	(2) (3.6.6)
36	runcic order-5 cubic (birapech) ↔	(1) (5.5.5)	-	(3) (3.4.5.4)	(1) (3.3.3)
37	runcicantic order-5 cubic (bitapech) ↔	(1) (3.10.10)	-	(2) (4.6.10)	(1) (3.6.6)

#	Honeycomb name Coxeter diagram ↔	Cells by location (and count around each vertex)				vertex figure	Picture
#	Honeycomb name Coxeter diagram ↔	0	1	3	Alt	vertex figure	Picture
[10]	Order-4 dodecahedral (doehon) ↔	(4) (5.5.5)	-	-
[11]	rectified order-4 dodecahedral (riddoh) ↔	(2) (3.5.3.5)	-	(2) (3.3.3.3)
[12]	rectified order-5 cubic (ripech) ↔	(1) (3.3.3.3.3)	-	(5) (3.4.3.4)
[15]	bitruncated order-5 cubic (ciddoh) ↔	(1) (5.6.6)	-	(2) (4.6.6)
[14]	truncated order-4 dodecahedral (tiddoh) ↔	(2) (3.10.10)	-	(1) (3.3.3.3)
[17]	cantellated order-4 dodecahedral (sriddoh) ↔	(1) (3.4.5.4)	(2) (4.4.4)	(1) (3.4.3.4)
[20]	cantitruncated order-4 dodecahedral (griddoh) ↔	(1) (4.6.10)	(1) (4.4.4)	(1) (4.6.6)
Nonuniform	snub rectified order-4 dodecahedral ↔	(2) (3.3.3.3.5)	(1) (3.3.3)	(2) (3.3.3.3.3)	(4) +(3.3.3)	Irr. tridiminished icosahedron

[(4,3,3,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group:

The bitruncated and runcinated forms (41 and 42) contain the faces of two regular skew polyhedrons: {8,6|3} and {6,8|3}.

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					vertex figure	Picture
#	Honeycomb name Coxeter diagram	0	1	2	3	Alt	vertex figure	Picture
38	tetrahedral-cubic (gadtatdic) {(3,3,3,4)}	(4) (3.3.3)	-	(4) (4.4.4)	(6) (3.4.3.4)
39	tetrahedral-octahedral (gacocaddit) {(3,3,4,3)}	(12) (3.3.3.3)	(8) (3.3.3)	-	(8) (3.3.3.3)
40	cyclotruncated tetrahedral-cubic (cytitch) ct{(3,3,3,4)}	(3) (3.6.6)	(1) (3.3.3)	(1) (4.4.4)	(3) (4.6.6)
41	cyclotruncated cube-tetrahedron (cyticth) ct{(4,3,3,3)}	(1) (3.3.3)	(1) (3.3.3)	(3) (3.8.8)	(3) (3.8.8)
42	cyclotruncated octahedral-tetrahedral (cytoth) ct{(3,3,4,3)}	(4) (3.6.6)	(4) (3.6.6)	(1) (3.3.3.3)	(1) (3.3.3.3)
43	rectified tetrahedral-cubic (ritch) r{(3,3,3,4)}	(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.4.3.4)	(2) (3.4.4.4)
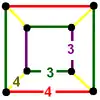44	truncated tetrahedral-cubic (titch) t{(3,3,3,4)}	(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.8.8)	(2) (4.6.8)
45	truncated tetrahedral-octahedral (titdoh) t{(3,3,4,3)}	(2) (4.6.6)	(1) (3.6.6)	(1) (3.4.4.4)	(1) (4.6.6)
46	omnitruncated tetrahedral-cubic (otitch) tr{(3,3,3,4)}	(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.8)	(1) (4.6.8)
Nonuniform	omnisnub tetrahedral-cubic sr{(3,3,3,4)}	(1) (3.3.3.3.3)	(1) (3.3.3.3.3)	(1) (3.3.3.3.4)	(1) (3.3.3.3.4)	(4) +(3.3.3)

[(5,3,3,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group:

The bitruncated and runcinated forms (50 and 51) contain the faces of two regular skew polyhedrons: {10,6|3} and {6,10|3}.

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				vertex figure	Picture
#	Honeycomb name Coxeter diagram	0	1	2	3	vertex figure	Picture
47	tetrahedral-dodecahedral	(4) (3.3.3)	-	(4) (5.5.5)	(6) (3.5.3.5)
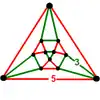48	tetrahedral-icosahedral	(30) (3.3.3.3)	(20) (3.3.3)	-	(12) (3.3.3.3.3)
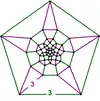49	cyclotruncated tetrahedral-dodecahedral	(3) (3.6.6)	(1) (3.3.3)	(1) (5.5.5)	(3) (5.6.6)
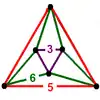52	rectified tetrahedral-dodecahedral	(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
53	truncated tetrahedral-dodecahedral	(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.10.10)	(2) (4.6.10)
54	truncated tetrahedral-icosahedral	(2) (4.6.6)	(1) (3.6.6)	(1) (3.4.5.4)	(1) (5.6.6)

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)			vertex figure	Picture
#	Honeycomb name Coxeter diagram	0,1	2,3	Alt	vertex figure	Picture
50	cyclotruncated dodecahedral-tetrahedral	(2) (3.3.3)	(6) (3.10.10)
51	cyclotruncated tetrahedral-icosahedral	(10) (3.6.6)	(2) (3.3.3.3.3)
55	omnitruncated tetrahedral-dodecahedral	(2) (4.6.6)	(2) (4.6.10)
Nonuniform	omnisnub tetrahedral-dodecahedral	(2) (3.3.3.3.3)	(2) (3.3.3.3.5)	(4) +(3.3.3)

[(4,3,4,3)] family

There are 6 forms, generated by ring permutations of the Coxeter group: . There are 4 extended symmetries possible based on the symmetry of the rings: , , , and .

This symmetry family is also related to a radical subgroup, index 6, ↔ , constructed by [(4,3,4,3^*)], and represents a trigonal trapezohedron fundamental domain.

The truncated forms (57 and 58) contain the faces of two regular skew polyhedrons: {6,6|4} and {8,8|3}.

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				vertex figure	Pictures
#	Honeycomb name Coxeter diagram	0	1	2	3	vertex figure	Pictures
56	cubic-octahedral (cohon)	(6) (3.3.3.3)	-	(8) (4.4.4)	(12) (3.4.3.4)
60	truncated cubic-octahedral (tucoh)	(1) (4.6.6)	(1) (3.4.4.4)	(1) (3.8.8)	(2) (4.6.8)

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)			vertex figure	Picture
#	Honeycomb name Coxeter diagram	0,3	1,2	Alt	vertex figure	Picture
57	cyclotruncated octahedral-cubic (cytoch)	(6) (4.6.6)	(2) (4.4.4)
Nonuniform	cyclosnub octahedral-cubic	(4) (3.3.3.3.3)	(2) (3.3.3)	(4) +(3.3.3.3)

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)		vertex figure	Picture
#	Honeycomb name Coxeter diagram	0,1	2,3	vertex figure	Picture
58	cyclotruncated cubic-octahedral (cytacoh)	(2) (3.3.3.3)	(6) (3.8.8)

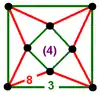#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)		vertex figure	Picture
#	Honeycomb name Coxeter diagram	0,2	1,3	vertex figure	Picture
59	rectified cubic-octahedral (racoh)	(2) (3.4.3.4)	(4) (3.4.4.4)

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)		vertex figure	Picture
#	Honeycomb name Coxeter diagram	0,1,2,3	Alt	vertex figure	Picture
61	omnitruncated cubic-octahedral (otacoh)	(4) (4.6.8)
Nonuniform	omnisnub cubic-octahedral	(4) (3.3.3.3.4)	(4) +(3.3.3)

[(4,3,5,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group:

The truncated forms (65 and 66) contain the faces of two regular skew polyhedrons: {10,6|3} and {6,10|3}.

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				vertex figure	Picture
#	Honeycomb name Coxeter diagram	0	1	2	3	vertex figure	Picture
62	octahedral-dodecahedral	(6) (3.3.3.3)	-	(8) (5.5.5)	(1) (3.5.3.5)
63	cubic-icosahedral	(30) (3.4.3.4)	(20) (4.4.4)	-	(12) (3.3.3.3.3)
64	cyclotruncated octahedral-dodecahedral	(3) (4.6.6)	(1) (4.4.4)	(1) (5.5.5)	(3) (5.6.6)
67	rectified octahedral-dodecahedral	(1) (3.4.3.4)	(2) (3.4.4.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
68	truncated octahedral-dodecahedral	(1) (4.6.6)	(1) (3.4.4.4)	(1) (3.10.10)	(2) (4.6.10)
69	truncated cubic-dodecahedral	(2) (4.6.8)	(1) (3.8.8)	(1) (3.4.5.4)	(1) (5.6.6)

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)			vertex figure	Picture
#	Honeycomb name Coxeter diagram	0,1	2,3	Alt	vertex figure	Picture
65	cyclotruncated dodecahedral-octahedral	(2) (3.3.3.3)	(8) (3.10.10)
66	cyclotruncated cubic-icosahedral	(10) (3.8.8)	(2) (3.3.3.3.3)
70	omnitruncated octahedral-dodecahedral	(2) (4.6.8)	(2) (4.6.10)
Nonuniform	omnisnub octahedral-dodecahedral	(2) (3.3.3.3.4)	(2) (3.3.3.3.5)	(4) +(3.3.3)

[(5,3,5,3)] family

There are 6 forms, generated by ring permutations of the Coxeter group: . There are 4 extended symmetries possible based on the symmetry of the rings: , , , and .

The truncated forms (72 and 73) contain the faces of two regular skew polyhedrons: {6,6|5} and {10,10|3}.

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					vertex figure	Picture
#	Honeycomb name Coxeter diagram	0	1	2	3	Alt	vertex figure	Picture
71	dodecahedral-icosahedral	(12) (3.3.3.3.3)	-	(20) (5.5.5)	(30) (3.5.3.5)
72	cyclotruncated icosahedral-dodecahedral	(3) (5.6.6)	(1) (5.5.5)	(1) (5.5.5)	(3) (5.6.6)
73	cyclotruncated dodecahedral-icosahedral	(1) (3.3.3.3.3)	(1) (3.3.3.3.3)	(3) (3.10.10)	(3) (3.10.10)
74	rectified dodecahedral-icosahedral	(1) (3.5.3.5)	(2) (3.4.5.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
75	truncated dodecahedral-icosahedral	(1) (5.6.6)	(1) (3.4.5.4)	(1) (3.10.10)	(2) (4.6.10)
76	omnitruncated dodecahedral-icosahedral	(1) (4.6.10)	(1) (4.6.10)	(1) (4.6.10)	(1) (4.6.10)
Nonuniform	omnisnub dodecahedral-icosahedral	(1) (3.3.3.3.5)	(1) (3.3.3.3.5)	(1) (3.3.3.3.5)	(1) (3.3.3.3.5)	(4) +(3.3.3)

Other non-Wythoffians

There are several other known non-Wythoffian uniform compact hyperbolic honeycombs, and it is not known how many are left to be discovered. Two have been listed above as diminishings of the icosahedral honeycomb {3,5,3}.^[7]

In 1997 Wendy Krieger discovered an infinite series of uniform hyperbolic honeycombs with pseudoicosahedral vertex figures, made from 8 cubes and 12 p-gonal prisms at a vertex for any integer p. In the case p = 4, all cells are cubes and the result is the order-5 cubic honeycomb.^[7]

Another two known ones are related to noncompact families. The tessellation consists of truncated cubes and infinite order-8 triangular tilings . However the latter intersect the sphere at infinity orthogonally, having exactly the same curvature as the hyperbolic space, and can be replaced by mirror images of the remainder of the tessellation, resulting in a compact uniform honeycomb consisting only of the truncated cubes. (So they are analogous to the hemi-faces of spherical hemipolyhedra.)^[7]^[8] Something similar can be done with the tessellation consisting of small rhombicuboctahedra , infinite order-8 triangular tilings , and infinite order-8 square tilings . The order-8 square tilings already intersect the sphere at infinity orthogonally, and if the order-8 triangular tilings are augmented with a set of triangular prisms, the surface passing through their centre points also intersects the sphere at infinity orthogonally. After replacing with mirror images, the result is a compact honeycomb containing the small rhombicuboctahedra and the triangular prisms.^[9]

Another non-Wythoffian was discovered in 2021. It has as vertex figure a snub cube with 8 vertices removed and contains two octahedra and eight snub cubes at each vertex.^[7] Subsequently Krieger found a non-Wythoffian with a snub cube as the vertex figure, containing 32 tetrahedra and 6 octahedra at each vertex, and that the truncated and rectified versions of this honeycomb are still uniform. In 2022, Richard Klitzing generalised this construction to use any snub as vertex figure: the result is compact for p=4 or 5 (with a snub cube or snub dodecahedral vertex figure respectively), paracompact for p=6 (with a snub trihexagonal tiling as the vertex figure), and hypercompact for p>6. Again, the truncated and rectified versions of these honeycombs are still uniform.^[7]

Summary enumeration of compact uniform honeycombs

This is the complete enumeration of the 76 Wythoffian uniform honeycombs. The alternations are listed for completeness, but most are non-uniform.

Index	Coxeter group	Extended symmetry	Honeycombs		Chiral extended symmetry	Alternation honeycombs
H₁	${\bar {BH}}_{3}$ [4,3,5]	[4,3,5]	15	\| \| \| \| \| \| \| \| \| \| \| \|	[1⁺,4,(3,5)⁺]	(2)	(= )
H₁	${\bar {BH}}_{3}$ [4,3,5]	[4,3,5]	15	\| \| \| \| \| \| \| \| \| \| \| \|	[4,3,5]⁺	(1)
H₂	${\bar {J}}_{3}$ [3,5,3]	[3,5,3]	6	\| \| \| \|
H₂	${\bar {J}}_{3}$ [3,5,3]	[2⁺[3,5,3]]	5	\|	[2⁺[3,5,3]]⁺	(1)
H₃	${\bar {DH}}_{3}$ [5,3^1,1]	[5,3^1,1]	4	\| \|
H₃	${\bar {DH}}_{3}$ [5,3^1,1]	[1[5,3^1,1]]=[5,3,4] ↔	(7)	\| \| \| \| \|	[1[5,3^1,1]]⁺ =[5,3,4]⁺	(1)
H₄	${\widehat {AB}}_{3}$ [(4,3,3,3)]	[(4,3,3,3)]	6	\| \| \| \|
H₄	${\widehat {AB}}_{3}$ [(4,3,3,3)]	[2⁺[(4,3,3,3)]]	3	\|	[2⁺[(4,3,3,3)]]⁺	(1)
H₅	${\bar {K}}_{3}$ [5,3,5]	[5,3,5]	6	\| \| \| \|
H₅	${\bar {K}}_{3}$ [5,3,5]	[2⁺[5,3,5]]	3	\|	[2⁺[5,3,5]]⁺	(1)
H₆	${\widehat {AH}}_{3}$ [(5,3,3,3)]	[(5,3,3,3)]	6	\| \| \| \|
H₆	${\widehat {AH}}_{3}$ [(5,3,3,3)]	[2⁺[(5,3,3,3)]]	3	\|	[2⁺[(5,3,3,3)]]⁺	(1)
H₇	${\widehat {BB}}_{3}$ [(3,4)^[2]]	[(3,4)^[2]]	2
		[2⁺[(3,4)^[2]]]	1
		[2⁺[(3,4)^[2]]]	1
		[2⁺[(3,4)^[2]]]	1		[2⁺[(3⁺,4)^[2]]]	(1)
		[(2,2)⁺[(3,4)^[2]]]	1		[(2,2)⁺[(3,4)^[2]]]⁺	(1)
H₈	${\widehat {BH}}_{3}$ [(5,3,4,3)]	[(5,3,4,3)]	6	\| \| \| \|
H₈	${\widehat {BH}}_{3}$ [(5,3,4,3)]	[2⁺[(5,3,4,3)]]	3	\|	[2⁺[(5,3,4,3)]]⁺	(1)
H₉	${\widehat {HH}}_{3}$ [(3,5)^[2]]	[(3,5)^[2]]	2
		[2⁺[(3,5)^[2]]]	1
		[2⁺[(3,5)^[2]]]	1
		[2⁺[(3,5)^[2]]]	1
		[(2,2)⁺[(3,5)^[2]]]	1		[(2,2)⁺[(3,5)^[2]]]⁺	(1)

Notes

↑ Humphreys, 1990, page 141, 6.9 List of hyperbolic Coxeter groups, figure 2
↑ Felikson, 2002
↑ Felikson, 2002
↑ Wendy Y. Krieger, Walls and bridges: The view from six dimensions, Symmetry: Culture and Science Volume 16, Number 2, pages 171–192 (2005)
1 2 "Spd{3,5,3".}
↑ "Pd{3,5,3".}
1 2 3 4 5 "Hyperbolic Tesselations".
↑ "x4x3o8o".
↑ "lt-o8o4xb3x".

References

James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space)
Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
Coxeter Decompositions of Hyperbolic Tetrahedra, arXiv/PDF, A. Felikson, December 2002
C. W. L. Garner, Regular Skew Polyhedra in Hyperbolic Three-Space Can. J. Math. 19, 1179–1186, 1967. PDF Archived 2015-04-02 at the Wayback Machine
Norman Johnson, Geometries and Transformations (2018), Chapters 11,12,13
N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups 1999, Volume 4, Issue 4, pp 329–353
N.W. Johnson, R. Kellerhals, J.G. Ratcliffe,S.T. Tschantz, Commensurability classes of hyperbolic Coxeter groups H³: p130.
Klitzing, Richard. "Hyperbolic honeycombs H3 compact".

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Humphreys, 1990, page 141, 6.9 List of hyperbolic Coxeter groups, figure 2

[2] Felikson, 2002

[3] Felikson, 2002

[4] Wendy Y. Krieger, Walls and bridges: The view from six dimensions, Symmetry: Culture and Science Volume 16, Number 2, pages 171–192 (2005)

[klitzing-5] 1 2 "Spd{3,5,3".}

[6] "Pd{3,5,3".}

[klitzing2-7] 1 2 3 4 5 "Hyperbolic Tesselations".

[klitzing3-8] "x4x3o8o".

[klitzing4-9] "lt-o8o4xb3x".

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Hyperbolic uniform honeycomb families

Compact uniform honeycomb families

Paracompact hyperbolic uniform honeycombs

[3,5,3] family

[5,3,4] family

[5,3,5] family

[5,31,1] family

[(4,3,3,3)] family

[(5,3,3,3)] family

[(4,3,4,3)] family

[(4,3,5,3)] family

[(5,3,5,3)] family

Other non-Wythoffians

Summary enumeration of compact uniform honeycombs

See also

Notes

References

[5,3^1,1] family