In geometry, Lemoine's problem is a straightedge and compass construction problem posed by French mathematician Émile Lemoine in 1868:^[1][2]

Given one vertex of each of the equilateral triangles placed on the sides of a triangle, construct the original triangle.

The problem was published as Question 864 in Nouvelles Annales de Mathématiques (Series 2, Volume 7 (1868), p 191). The chief interest in the problem is that a discussion of the solution of the problem by Ludwig Kiepert published in Nouvelles Annales de Mathématiques (series 2, Volume 8 (1869), pp 40–42) contained a description of a hyperbola which is now known as the Kiepert hyperbola.^[3]

Ludwig Kiepert's solution

Diagram illustrating Lemma 1 .

Diagram illustrating Ludwig Kiepert's solution to Lemoine's problem

Kiepert establishes the validity of his construction by proving a few lemmas.^[3][4]

Problem

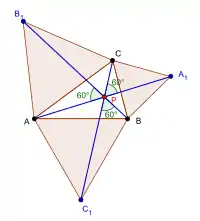
Let A₁, B₁, C₁ be the vertices of the equilateral triangles placed on the sides of a triangle ${\displaystyle \triangle ABC.}$ Given A₁, B₁, C₁ construct A, B, C.

Lemma 1

If on the three sides of an arbitrary triangle ${\displaystyle \triangle ABC,}$ one describes equilateral triangles ${\displaystyle \triangle ABC_{1},}$ ${\displaystyle \triangle ACB_{1},}$ ${\displaystyle \triangle BCA_{1},}$ then the line segments ${\displaystyle {\overline {AA_{1}}},}$ ${\displaystyle {\overline {BB_{1}}},}$ ${\displaystyle {\overline {CC_{1}}}}$ are equal, they concur in a point P, and the angles they form one another are equal to 60°.

Lemma 2

If on ${\displaystyle \triangle A_{1}B_{1}C_{1}}$ one makes the same construction as that on ${\displaystyle \triangle ABC,}$ there will have three equilateral triangles ${\displaystyle \triangle A_{1}B_{1}C_{2},}$ ${\displaystyle \triangle A_{1}C_{1}B_{2},}$ ${\displaystyle \triangle B_{1}C_{1}A_{2},}$ three equal line segments ${\displaystyle {\overline {A_{1}A_{2}}},}$ ${\displaystyle {\overline {B_{2}B_{2}}},}$ ${\displaystyle {\overline {C_{2}C_{2}}},}$ which will also concur at the point P.

Lemma 3

A, B, C are respectively the midpoints of ${\displaystyle {\overline {A_{1}A_{2}}},}$ ${\displaystyle {\overline {B_{2}B_{2}}},}$ ${\displaystyle {\overline {C_{2}C_{2}}}.}$

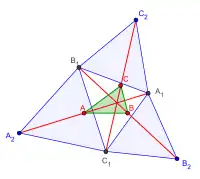
Solution

• Describe on the segments ${\displaystyle {\overline {A_{1}B_{1}}},}$ ${\displaystyle {\overline {A_{1}C_{1}}},}$ ${\displaystyle {\overline {B_{1}C_{1}}}}$ the equilateral triangles ${\displaystyle \triangle A_{1}B_{1}C_{1},}$ ${\displaystyle \triangle A_{1}C_{2}B_{2},}$ ${\displaystyle \triangle B_{1}C_{1}A_{2},}$ respectively.
• The midpoints of ${\displaystyle {\overline {A_{1}A_{2}}},}$ ${\displaystyle {\overline {B_{2}B_{2}}},}$ ${\displaystyle {\overline {C_{2}C_{2}}}}$ are, respectively, the vertices A, B, C of the required triangle.

Other solutions

Several other people in addition to Kiepert submitted their solutions during 1868–9, including Messrs Williere (at Arlon), Brocard, Claverie (Lycee de Clermont), Joffre (Lycee Charlemagne), Racine (Lycee de Poitiers), Augier (Lycee de Caen), V. Niebylowski, and L. Henri Lorrez. Kiepert's solution was more complete than the others.^[3]

References