The Mikheyev–Smirnov–Wolfenstein effect (often referred to as the matter effect) is a particle physics process which modifies neutrino oscillations in matter of varying density. The MSW effect is broadly analogous to the differential retardation of sound waves in density-variable media, however it also involves the propagation dynamics of three separate quantum fields which experience distortion.

In free space, the separate rates of neutrino eigenstates lead to standard neutrino flavor oscillation. Within matter – such as within the Sun – the analysis is more complicated, as shown by Mikheyev, Smirnov and Wolfenstein. It leads to a wide admixture of emanating neutrino flavors, which provides a compelling solution to the solar neutrino problem.

Works in 1978 and 1979 by American physicist Lincoln Wolfenstein led to understanding that the oscillation parameters of neutrinos are changed in matter. In 1985, the Soviet physicists Stanislav Mikheyev and Alexei Smirnov predicted that a slow decrease of the density of matter can resonantly enhance the neutrino mixing.^[1] Later in 1986, Stephen Parke of Fermilab, Hans Bethe of Cornell University, and S. Peter Rosen and James Gelb of Los Alamos National Laboratory provided analytic treatments of this effect.

Summary

The presence of electrons in matter changes the instantaneous Hamiltonian eigenstates (mass eigenstates) of neutrinos due to the charged current's elastic forward scattering of the electron neutrinos (i.e., weak interactions). This coherent forward scattering is analogous to the electromagnetic process leading to the refractive index of light in a medium and can be described either as the classical refractive index, ${\displaystyle n_{ref}}$ or the electric potential, ${\displaystyle V}$. The difference of potentials for different neutrinos ${\displaystyle \nu _{1}}$ and ${\displaystyle \nu _{2}}$: ${\displaystyle V=V_{1}-V_{2}}$ induces the evolution of mixed neutrino flavors (either electron, muon, or tau).

In the presence of matter, the Hamiltonian of the system changes with respect to the potential: ${\displaystyle H=H_{0}+V}$, where ${\displaystyle H_{0}}$ is the Hamiltonian in vacuum. Correspondingly, the mass eigenstates and eigenvalues of ${\displaystyle H}$ change, which means that the neutrinos in matter now have a different effective mass than they did in vacuum: ${\displaystyle \nu _{1},\nu _{2}\rightarrow \nu _{1m},\nu _{2m}}$. Since neutrino oscillations depend upon the squared mass difference of the neutrinos, neutrino oscillations experience different dynamics than they did in vacuum.

Similar to the vacuum case, the mixing angle ${\displaystyle \theta _{m}}$ describes the change of flavors of the eigenstates. In matter, the mixing angle depends on the number density of electrons ${\displaystyle n_{e}}$ and the energy of the neutrinos: ${\displaystyle \theta _{m}(x)=\theta _{m}(n_{e}(x))}$. As the neutrinos propagate through density-variant matter, ${\displaystyle \theta _{m}}$ changes – and with it, the flavors of the eigenstates.

With antineutrinos, the conceptual point is the same but the effective charge that the weak interaction couples to (called weak isospin) has an opposite sign. If the electron density of matter changes along the path of neutrinos, the mixing of neutrinos grows to maximum at some value of the density, and then turns back; it leads to resonant conversion of one type of neutrinos to another one.

The effect is important at the very large electron densities of the Sun where electron neutrinos are produced. The high-energy neutrinos seen, for example, in Sudbury Neutrino Observatory (SNO) and in Super-Kamiokande, are produced mainly as the higher mass eigenstate in matter ${\displaystyle \nu _{2m}}$, and remain as such as the density of solar material changes.^[2] Thus, the neutrinos of high energy leaving the Sun are in a vacuum propagation eigenstate, ${\displaystyle \nu _{2m}}$, that has a reduced overlap with the electron neutrino ${\displaystyle \nu _{\text{e}}=\nu _{1m}\cos \theta _{m}+\nu _{2m}\sin \theta _{m}}$ seen by charged current reactions in the detectors.

Resonance in the MSW effect

Neutrino flavor mixing experiences resonance and becomes maximal under certain conditions of the relationship between the vacuum oscillation length ${\displaystyle \ \ell _{\nu }={\frac {\ 4\pi \ E\ }{\Delta m^{2}}}\ }$ and the matter density-dependent refraction length ${\displaystyle \ \ell _{0}={\frac {{\sqrt {2\ }}\pi }{\ G_{f}\ n_{e}\ }}\ ,}$ where ${\displaystyle \ G_{f}\ }$ is the Fermi coupling constant. The refraction length ${\displaystyle \ \ell _{0}\ }$ is understood as the distance over which the matter "phase" from the coherent scattering is equal to ${\displaystyle \ 2\pi ~.}$

The resonance condition is given by ${\displaystyle \ \ell _{\nu }=\ell _{0}\cos(\theta )\ ,}$ which is when the neutrino system experiences resonance and the mixing becomes maximal. For very small ${\displaystyle \ \theta \ ,}$ this condition becomes ${\displaystyle \ \ell _{\nu }\approx \ell _{0}\ ,}$ that is, the eigenfrequency for a system of mixed neutrinos becomes approximately equal to the eigenfrequency of medium.

The resonance density ${\displaystyle \ n_{r}\ }$ is informed by the resonance condition: ${\displaystyle \ n_{r}={\frac {\Delta m^{2}}{\ 2{\sqrt {2\ }}E\ G_{f}\ }}\ \cos(2\theta )\ }$ and is directly related the number density of electrons ${\displaystyle \ n_{e}~.}$ If vacuum density reaches the maximal value, ${\displaystyle \ \theta ={\frac {\pi }{\ 4\ }}\ ,}$ the resonance density goes to zero. In a medium with fluctuating density, ${\displaystyle \ n_{r}\ }$ itself fluctuates – the interval between its maximum and minimum values is called the resonance layer.

Solar neutrinos and the MSW effect

For high-energy solar neutrinos the MSW effect is important, and leads to the expectation that ${\displaystyle P_{\text{ee}}=\sin ^{2}\theta _{s}}$, where ${\displaystyle \theta _{s}}$ is the solar mixing angle. This was dramatically confirmed in the Sudbury Neutrino Observatory (SNO), which has resolved the solar neutrino problem. SNO measured the flux of solar electron neutrinos to be ~34% of the total neutrino flux (the electron neutrino flux measured via the charged current reaction, and the total flux via the neutral current reaction). The SNO results agree well with the expectations. Earlier, Kamiokande and Super-Kamiokande measured a mixture of charged current and neutral current reactions, that also support the occurrence of the MSW effect with a similar suppression, but with less confidence.

Survival probability of solar neutrinos as predicted by the MSW theory. The continuous line is for neutrinos that are detected in the day, the dotted one for neutrinos that are detected in the night and that pass through the Earth, experiencing "regeneration". The 4 vertical strips indicate the values of the energies at which the survival probability was measured, by means of pp, ⁷Be, pep, and ⁸B solar neutrinos, respectively.

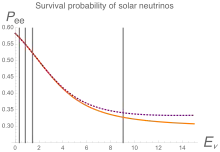
For the low-energy solar neutrinos, on the other hand, the matter effect is negligible, and the formalism of oscillations in vacuum is valid. The size of the source (i.e. the solar core) is significantly larger than the oscillation length, therefore, averaging over the oscillation factor, one obtains ${\displaystyle P_{\text{ee}}=1-{\tfrac {1}{2}}\sin ^{2}\left(2\theta _{s}\right)}$. For ${\displaystyle \theta _{s}}$ = 34° this corresponds to a survival probability of P_ee ≈ 60%. This is consistent with the experimental observations of low energy solar neutrinos by the Homestake experiment (the first experiment to reveal the solar neutrino problem), followed by GALLEX, GNO, and SAGE (collectively, gallium radiochemical experiments), and, more recently, the Borexino experiment, which observed the neutrinos from pp (< 420 keV), ⁷Be (862 keV), pep (1.44 MeV), and ⁸B (< 15 MeV) separately. The measurements of Borexino alone verify the MSW pattern; however all these experiments are consistent with each other and provide us strong evidence of the MSW effect.

These results are further supported by the reactor experiment KamLAND, that is uniquely able to measure the parameters of oscillation that are also consistent with all other measurements.

The transition between the low energy regime (the MSW effect is negligible) and the high energy regime (the oscillation probability is determined by matter effects) lies in the region of about 2 MeV for the solar neutrinos.

The MSW effect can also modify neutrino oscillations in the Earth, and future search for new oscillations and/or leptonic CP violation may make use of this property.

Supernova neutrinos and the MSW effect

Supernovae are calculated to emit of the order of ${\displaystyle 10^{58}}$ neutrinos and antineutrinos of all flavors,^[3] and supernova neutrinos carry away about 99% of the gravitational energy of the supernova and are considered strongest source of cosmic neutrinos in the MeV range.^[4] As such, scientists have attempted to simulate and mathematically characterize the action of MSW dynamics on SN neutrinos.

Some effect of MSW flavor conversion has already been observed in SN 1987A. In the case of normal neutrino mass hierarchy, ${\displaystyle \nu _{e}\rightarrow \nu _{1}}$and ${\displaystyle \nu _{\mu ,\tau }\rightarrow \nu _{2}}$, transitions occurred inside the star, then ${\displaystyle \nu _{1}}$ and ${\displaystyle \nu _{2}}$ oscillated inside the Earth. Due to the differences in the distance traveled by neutrinos to Kamiokande, IMB and Baksan within the Earth, the MSW effect can partially explain the difference of the Kamiokande and IMB energy spectrum of events.^[5]

See also

• Neutrino oscillations

References

Bibliography