Matsubara frequency

In thermal quantum field theory, the Matsubara frequency summation (named after Takeo Matsubara) is the summation over discrete imaginary frequencies. It takes the following form

S_{\eta }={\frac {1}{\beta }}\sum _{i\omega _{n}}g(i\omega _{n}),

where $\beta =\hbar /k_{\rm {B}}T$ is the inverse temperature and the frequencies $\omega _{n}$ are usually taken from either of the following two sets (with $n\in \mathbb {Z}$ ):

bosonic frequencies:

\omega _{n}={\frac {2n\pi }{\beta }},

fermionic frequencies:

\omega _{n}={\frac {(2n+1)\pi }{\beta }},

The summation will converge if $g(z=i\omega )$ tends to 0 in $z\to \infty$ limit in a manner faster than $z^{-1}$ . The summation over bosonic frequencies is denoted as $S_{\rm {B}}$ (with $\eta =+1$ ), while that over fermionic frequencies is denoted as $S_{\rm {F}}$ (with $\eta =-1$ ). $\eta$ is the statistical sign.

In addition to thermal quantum field theory, the Matsubara frequency summation method also plays an essential role in the diagrammatic approach to solid-state physics, namely, if one considers the diagrams at finite temperature.^[1] ^[2] ^[3]

Generally speaking, if at $T=0\,{\text{K}}$ , a certain Feynman diagram is represented by an integral $\int _{T=0}\mathrm {d} \omega \ g(\omega )$ , at finite temperature it is given by the sum $S_{\eta }$ .

Summation formalism

General formalism

Figure 1.

Figure 2.

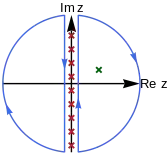
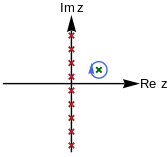
The trick to evaluate Matsubara frequency summation is to use a Matsubara weighting function h_η(z) that has simple poles located exactly at $z=i\omega _{n}$ .^[3] The weighting functions in the boson case η = +1 and fermion case η = −1 differ. The choice of weighting function will be discussed later. With the weighting function, the summation can be replaced by a contour integral surrounding the imaginary axis.

S_{\eta }={\frac {1}{\beta }}\sum _{i\omega }g(i\omega )={\frac {1}{2\pi i\beta }}\oint g(z)h_{\eta }(z)\,dz,

As in Fig. 1, the weighting function generates poles (red crosses) on the imaginary axis. The contour integral picks up the residue of these poles, which is equivalent to the summation. This procedure is sometimes called Sommerfeld-Watson transformation.^[4]

By deformation of the contour lines to enclose the poles of g(z) (the green cross in Fig. 2), the summation can be formally accomplished by summing the residue of g(z)h_η(z) over all poles of g(z),

S_{\eta }=-{\frac {1}{\beta }}\sum _{z_{0}\in g(z){\text{ poles}}}\operatorname {Res} g(z_{0})h_{\eta }(z_{0}).

Note that a minus sign is produced, because the contour is deformed to enclose the poles in the clockwise direction, resulting in the negative residue.

Choice of Matsubara weighting function

To produce simple poles on boson frequencies $z=i\omega _{n}$ , either of the following two types of Matsubara weighting functions can be chosen

h_{\rm {B}}^{(1)}(z)={\frac {\beta }{1-e^{-\beta z}}}=-\beta n_{\rm {B}}(-z)=\beta (1+n_{\rm {B}}(z)),

h_{\rm {B}}^{(2)}(z)={\frac {-\beta }{1-e^{\beta z}}}=\beta n_{\rm {B}}(z),

depending on which half plane the convergence is to be controlled in. $h_{\rm {B}}^{(1)}(z)$ controls the convergence in the left half plane (Re z < 0), while $h_{\rm {B}}^{(2)}(z)$ controls the convergence in the right half plane (Re z > 0). Here $n_{\rm {B}}(z)=(e^{\beta z}-1)^{-1}$ is the Bose–Einstein distribution function.

The case is similar for fermion frequencies. There are also two types of Matsubara weighting functions that produce simple poles at $z=i\omega _{m}$

h_{\rm {F}}^{(1)}(z)={\frac {\beta }{1+e^{-\beta z}}}=\beta n_{\rm {F}}(-z)=\beta (1-n_{\rm {F}}(z)),

h_{\rm {F}}^{(2)}(z)={\frac {-\beta }{1+e^{\beta z}}}=-\beta n_{\rm {F}}(z).

$h_{\rm {F}}^{(1)}(z)$ controls the convergence in the left half plane (Re z < 0), while $h_{\rm {F}}^{(2)}(z)$ controls the convergence in the right half plane (Re z > 0). Here $n_{\rm {F}}(z)=(e^{\beta z}+1)^{-1}$ is the Fermi–Dirac distribution function.

In the application to Green's function calculation, g(z) always have the structure

g(z)=G(z)e^{-z\tau },

which diverges in the left half plane given 0 < τ < β. So as to control the convergence, the weighting function of the first type is always chosen $h_{\eta }(z)=h_{\eta }^{(1)}(z)$ . However, there is no need to control the convergence if the Matsubara summation does not diverge. In that case, any choice of the Matsubara weighting function will lead to identical results.

Table of Matsubara frequency summations

The following table contains $S_{\eta }={\frac {1}{\beta }}\sum _{i\omega }g(i\omega )$ for some simple rational functions g(z). The symbol η = ±1 is the statistical sign, +1 for bosons and -1 for fermions.

$g(i\omega )$	$S_{\eta }$
$(i\omega -\xi )^{-1}$	$-\eta n_{\eta }(\xi )$ ^[1]
$(i\omega -\xi )^{-2}$	$-\eta n_{\eta }^{\prime }(\xi )=\beta n_{\eta }(\xi )(\eta +n_{\eta }(\xi ))$
$(i\omega -\xi )^{-n}$	$-{\frac {\eta }{(n-1)!}}\partial _{\xi }^{n-1}n_{\eta }(\xi )$
${\frac {1}{(i\omega -\xi _{1})(i\omega -\xi _{2})}}$	$-{\frac {\eta (n_{\eta }(\xi _{1})-n_{\eta }(\xi _{2}))}{\xi _{1}-\xi _{2}}}$
${\frac {1}{(i\omega -\xi _{1})^{2}(i\omega -\xi _{2})^{2}}}$	${\frac {\eta }{(\xi _{1}-\xi _{2})^{2}}}\left({\frac {2(n_{\eta }(\xi _{1})-n_{\eta }(\xi _{2}))}{\xi _{1}-\xi _{2}}}-(n_{\eta }^{\prime }(\xi _{1})+n_{\eta }^{\prime }(\xi _{2}))\right)$
${\frac {1}{(i\omega -\xi _{1})^{2}-\xi _{2}^{2}}}$	$\eta c_{\eta }(\xi _{1},\xi _{2})$
${\frac {1}{(i\omega )^{2}-\xi ^{2}}}$	$\eta c_{\eta }(0,\xi )=-{\frac {1}{2\xi }}(1+2\eta n_{\eta }(\xi ))$
${\frac {(i\omega )^{2}}{(i\omega )^{2}-\xi ^{2}}}$	$-{\frac {\xi }{2}}(1+2\eta n_{\eta }(\xi ))$ ^[1]
${\frac {1}{((i\omega )^{2}-\xi ^{2})^{2}}}$	$-{\frac {\eta }{2\xi ^{2}}}(c_{\eta }(0,\xi )+n_{\eta }^{\prime }(\xi ))$
${\frac {(i\omega )^{2}}{((i\omega )^{2}-\xi ^{2})^{2}}}$	${\frac {\eta }{2}}(c_{\eta }(0,\xi )-n_{\eta }^{\prime }(\xi ))$
${\frac {(i\omega )^{2}+\xi ^{2}}{((i\omega )^{2}-\xi ^{2})^{2}}}$	$-\eta n_{\eta }^{\prime }(\xi )=\beta n_{\eta }(\xi )(\eta +n_{\eta }(\xi ))$
${\frac {1}{((i\omega )^{2}-\xi _{1}^{2})((i\omega )^{2}-\xi _{2}^{2})}}$	${\frac {\eta (c_{\eta }(0,\xi _{1})-c_{\eta }(0,\xi _{2}))}{\xi _{1}^{2}-\xi _{2}^{2}}}$
$\left({\frac {1}{(i\omega )^{2}-\xi _{1}^{2}}}+{\frac {1}{(i\omega )^{2}-\xi _{2}^{2}}}\right)^{2}$	$\eta \left({\frac {3\xi _{1}^{2}+\xi _{2}^{2}}{2\xi _{1}^{2}(\xi _{1}^{2}-\xi _{2}^{2})}}c_{\eta }(0,\xi _{1})-{\frac {n_{\eta }^{\prime }(\xi _{1})}{2\xi _{1}^{2}}}\right)+(1\leftrightarrow 2)$ ^[2]
$\left({\frac {1}{(i\omega )^{2}-\xi _{1}^{2}}}-{\frac {1}{(i\omega )^{2}-\xi _{2}^{2}}}\right)^{2}$	$\eta \left(-{\frac {5\xi _{1}^{2}-\xi _{2}^{2}}{2\xi _{1}^{2}(\xi _{1}^{2}-\xi _{2}^{2})}}c_{\eta }(0,\xi _{1})-{\frac {n_{\eta }^{\prime }(\xi _{1})}{2\xi _{1}^{2}}}\right)+(1\leftrightarrow 2)$ ^[2]

[1] Since the summation does not converge, the result may differ upon different choice of the Matsubara weighting function.

[2] (1 ↔ 2) denotes the same expression as the before but with index 1 and 2 interchanged.

Applications in physics

Zero temperature limit

In this limit $\beta \rightarrow \infty$ , the Matsubara frequency summation is equivalent to the integration of imaginary frequency over imaginary axis.

{\frac {1}{\beta }}\sum _{i\omega }=\int _{-i\infty }^{i\infty }{\frac {\mathrm {d} (i\omega )}{2\pi i}}.

Some of the integrals do not converge. They should be regularized by introducing the frequency cutoff $\Omega$ , and then subtracting the divergent part ( $\Omega$ -dependent) from the integral before taking the limit of $\Omega \rightarrow \infty$ . For example, the free energy is obtained by the integral of logarithm,

\eta \lim _{\Omega \rightarrow \infty }\left[\int _{-i\Omega }^{i\Omega }{\frac {\mathrm {d} (i\omega )}{2\pi i}}\left(\ln(-i\omega +\xi )-{\frac {\pi \xi }{2\Omega }}\right)-{\frac {\Omega }{\pi }}(\ln \Omega -1)\right]=\left\{{\begin{array}{cc}0&\xi \geq 0,\\-\eta \xi &\xi <0,\end{array}}\right.

meaning that at zero temperature, the free energy simply relates to the internal energy below the chemical potential. Also the distribution function is obtained by the following integral

\eta \lim _{\Omega \rightarrow \infty }\int _{-i\Omega }^{i\Omega }{\frac {\mathrm {d} (i\omega )}{2\pi i}}\left({\frac {1}{-i\omega +\xi }}-{\frac {\pi }{2\Omega }}\right)=\left\{{\begin{array}{cc}0&\xi \geq 0,\\-\eta &\xi <0,\end{array}}\right.

which shows step function behavior at zero temperature.

Green's function related

Time domain

Consider a function G(τ) defined on the imaginary time interval (0,β). It can be given in terms of Fourier series,

G(\tau )={\frac {1}{\beta }}\sum _{i\omega }G(i\omega )e^{-i\omega \tau },

where the frequency only takes discrete values spaced by 2 $π$ /β.

The particular choice of frequency depends on the boundary condition of the function G(τ). In physics, G(τ) stands for the imaginary time representation of Green's function

G(\tau )=-\langle {\mathcal {T}}_{\tau }\psi (\tau )\psi ^{*}(0)\rangle .

It satisfies the periodic boundary condition G(τ+β)=G(τ) for a boson field. While for a fermion field the boundary condition is anti-periodic G(τ + β) = −G(τ).

Given the Green's function G(iω) in the frequency domain, its imaginary time representation G(τ) can be evaluated by Matsubara frequency summation. Depending on the boson or fermion frequencies that is to be summed over, the resulting G(τ) can be different. To distinguish, define

G_{\eta }(\tau )={\begin{cases}G_{\rm {B}}(\tau ),&{\text{if }}\eta =+1,\\G_{\rm {F}}(\tau ),&{\text{if }}\eta =-1,\end{cases}}

with

G_{\rm {B}}(\tau )={\frac {1}{\beta }}\sum _{i\omega _{n}}G(i\omega _{n})e^{-i\omega _{n}\tau },

G_{\rm {F}}(\tau )={\frac {1}{\beta }}\sum _{i\omega _{m}}G(i\omega _{m})e^{-i\omega _{m}\tau }.

Note that τ is restricted in the principal interval (0,β). The boundary condition can be used to extend G(τ) out of the principal interval. Some frequently used results are concluded in the following table.

$G(i\omega )$	$G_{\eta }(\tau )$
$(i\omega -\xi )^{-1}$	$-e^{\xi (\beta -\tau )}n_{\eta }(\xi )$
$(i\omega -\xi )^{-2}$	$e^{\xi (\beta -\tau )}n_{\eta }(\xi )\left(\tau +\eta \beta n_{\eta }(\xi )\right)$
$(i\omega -\xi )^{-3}$	$-{\frac {1}{2}}e^{\xi (\beta -\tau )}n_{\eta }(\xi )\left(\tau ^{2}+\eta \beta (\beta +2\tau )n_{\eta }(\xi )+2\beta ^{2}n_{\eta }^{2}(\xi )\right)$
$(i\omega -\xi _{1})^{-1}(i\omega -\xi _{2})^{-1}$	$-{\frac {e^{\xi _{1}(\beta -\tau )}n_{\eta }(\xi _{1})-e^{\xi _{2}(\beta -\tau )}n_{\eta }(\xi _{2})}{\xi _{1}-\xi _{2}}}$
$(\omega ^{2}+m^{2})^{-1}$	${\frac {e^{-m\tau }}{2m}}+{\frac {\eta }{m}}\cosh {m\tau }\;n_{\eta }(m)$
$i\omega (\omega ^{2}+m^{2})^{-1}$	${\frac {e^{-m\tau }}{2}}-\eta \,\sinh {m\tau }\;n_{\eta }(m)$

Operator switching effect

The small imaginary time plays a critical role here. The order of the operators will change if the small imaginary time changes sign.

\langle \psi \psi ^{*}\rangle =\langle {\mathcal {T}}_{\tau }\psi (\tau =0^{+})\psi ^{*}(0)\rangle =-G_{\eta }(\tau =0^{+})=-{\frac {1}{\beta }}\sum _{i\omega }G(i\omega )e^{-i\omega 0^{+}}

\langle \psi ^{*}\psi \rangle =\eta \langle {\mathcal {T}}_{\tau }\psi (\tau =0^{-})\psi ^{*}(0)\rangle =-\eta G_{\eta }(\tau =0^{-})=-{\frac {\eta }{\beta }}\sum _{i\omega }G(i\omega )e^{i\omega 0^{+}}

Distribution function

The evaluation of distribution function becomes tricky because of the discontinuity of Green's function G(τ) at τ = 0. To evaluate the summation

G(0)=\sum _{i\omega }(i\omega -\xi )^{-1},

both choices of the weighting function are acceptable, but the results are different. This can be understood if we push G(τ) away from τ = 0 a little bit, then to control the convergence, we must take $h_{\eta }^{(1)}(z)$ as the weighting function for $G(\tau =0^{+})$ , and $h_{\eta }^{(2)}(z)$ for $G(\tau =0^{-})$ .

Bosons

G_{\rm {B}}(\tau =0^{-})={\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {e^{i\omega _{n}0^{+}}}{i\omega _{n}-\xi }}=-n_{\rm {B}}(\xi ),

G_{\rm {B}}(\tau =0^{+})={\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {e^{-i\omega _{n}0^{+}}}{i\omega _{n}-\xi }}=-(n_{\rm {B}}(\xi )+1).

Fermions

G_{\rm {F}}(\tau =0^{-})={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {e^{i\omega _{m}0^{+}}}{i\omega _{m}-\xi }}=n_{\rm {F}}(\xi ),

G_{\rm {F}}(\tau =0^{+})={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {e^{-i\omega _{m}0^{+}}}{i\omega _{m}-\xi }}=-(1-n_{\rm {F}}(\xi )).

Free energy

Bosons

{\frac {1}{\beta }}\sum _{i\omega _{n}}\ln(\beta (-i\omega _{n}+\xi ))={\frac {1}{\beta }}\ln(1-e^{-\beta \xi }),

Fermions

-{\frac {1}{\beta }}\sum _{i\omega _{m}}\ln(\beta (-i\omega _{m}+\xi ))=-{\frac {1}{\beta }}\ln(1+e^{-\beta \xi }).

Diagram evaluations

Frequently encountered diagrams are evaluated here with the single mode setting. Multiple mode problems can be approached by a spectral function integral.

Fermion self energy

\Sigma (i\omega _{m})=-{\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {1}{i\omega _{m}+i\omega _{n}-\varepsilon }}{\frac {1}{i\omega _{n}-\Omega }}=-{\frac {n_{\rm {B}}(\varepsilon )+n_{\rm {F}}(\Omega )}{i\omega _{m}-\varepsilon +\Omega }}.

Particle-hole bubble

\Pi (i\omega _{n})={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {1}{i\omega _{m}+i\omega _{n}-\varepsilon }}{\frac {1}{i\omega _{m}-\varepsilon '}}={\frac {n_{\rm {B}}(\varepsilon )+n_{\rm {F}}\left(\varepsilon '\right)}{i\omega _{n}-\varepsilon +\varepsilon '}}.

Particle-particle bubble

\Pi (i\omega _{n})=-{\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {1}{i\omega _{m}+i\omega _{n}-\varepsilon }}{\frac {1}{-i\omega _{m}-\varepsilon '}}={\frac {1-n_{\rm {F}}\left(\varepsilon '\right)+n_{\rm {B}}(\varepsilon )}{i\omega _{n}-\varepsilon -\varepsilon '}}.

Appendix: Properties of distribution functions

Distribution functions

The general notation $n_{\eta }$ stands for either Bose (η = +1) or Fermi (η = −1) distribution function

n_{\eta }(\xi )={\frac {1}{e^{\beta \xi }-\eta }}.

If necessary, the specific notations n_B and n_F are used to indicate Bose and Fermi distribution functions respectively

n_{\eta }(\xi )={\begin{cases}n_{\rm {B}}(\xi ),&{\text{if }}\eta =+1,\\n_{\rm {F}}(\xi ),&{\text{if }}\eta =-1.\end{cases}}

Relation to hyperbolic functions

The Bose distribution function is related to hyperbolic cotangent function by

n_{\rm {B}}(\xi )={\frac {1}{2}}\left(\operatorname {coth} {\frac {\beta \xi }{2}}-1\right).

The Fermi distribution function is related to hyperbolic tangent function by

n_{\rm {F}}(\xi )={\frac {1}{2}}\left(1-\operatorname {tanh} {\frac {\beta \xi }{2}}\right).

Parity

Both distribution functions do not have definite parity,

n_{\eta }(-\xi )=-\eta -n_{\eta }(\xi ).

Another formula is in terms of the $c_{\eta }$ function

n_{\eta }(-\xi )=n_{\eta }(\xi )+2\xi c_{\eta }(0,\xi ).

However their derivatives have definite parity.

Bose–Fermi transmutation

Bose and Fermi distribution functions transmute under a shift of the variable by the fermionic frequency,

n_{\eta }(i\omega _{m}+\xi )=-n_{-\eta }(\xi ).

However shifting by bosonic frequencies does not make any difference.

Derivatives

First order

n_{\rm {B}}^{\prime }(\xi )=-{\frac {\beta }{4}}\mathrm {csch} ^{2}{\frac {\beta \xi }{2}},

n_{\rm {F}}^{\prime }(\xi )=-{\frac {\beta }{4}}\mathrm {sech} ^{2}{\frac {\beta \xi }{2}}.

In terms of product:

n_{\eta }^{\prime }(\xi )=-\beta n_{\eta }(\xi )(1+\eta n_{\eta }(\xi )).

In the zero temperature limit:

n_{\eta }^{\prime }(\xi )=\eta \delta (\xi ){\text{ as }}\beta \rightarrow \infty .

Second order

n_{\rm {B}}^{\prime \prime }(\xi )={\frac {\beta ^{2}}{4}}\operatorname {csch} ^{2}{\frac {\beta \xi }{2}}\operatorname {coth} {\frac {\beta \xi }{2}},

n_{\rm {F}}^{\prime \prime }(\xi )={\frac {\beta ^{2}}{4}}\operatorname {sech} ^{2}{\frac {\beta \xi }{2}}\operatorname {tanh} {\frac {\beta \xi }{2}}.

Formula of difference

n_{\eta }(a+b)-n_{\eta }(a-b)=-{\frac {\mathrm {sinh} \beta b}{\mathrm {cosh} \beta a-\eta \,\mathrm {cosh} \beta b}}.

Case a = 0

n_{\rm {B}}(b)-n_{\rm {B}}(-b)=\mathrm {coth} {\frac {\beta b}{2}},

n_{\rm {F}}(b)-n_{\rm {F}}(-b)=-\mathrm {tanh} {\frac {\beta b}{2}}.

Case a → 0

n_{\rm {B}}(a+b)-n_{\rm {B}}(a-b)=\operatorname {coth} {\frac {\beta b}{2}}+n_{\rm {B}}^{\prime \prime }(b)a^{2}+\cdots ,

n_{\rm {F}}(a+b)-n_{\rm {F}}(a-b)=-\operatorname {tanh} {\frac {\beta b}{2}}+n_{\rm {F}}^{\prime \prime }(b)a^{2}+\cdots .

Case b → 0

n_{\rm {B}}(a+b)-n_{\rm {B}}(a-b)=2n_{\rm {B}}^{\prime }(a)b+\cdots ,

n_{\rm {F}}(a+b)-n_{\rm {F}}(a-b)=2n_{\rm {F}}^{\prime }(a)b+\cdots .

The function c_η

Definition:

c_{\eta }(a,b)\equiv -{\frac {n_{\eta }(a+b)-n_{\eta }(a-b)}{2b}}.

For Bose and Fermi type:

c_{\rm {B}}(a,b)\equiv c_{+}(a,b),

c_{\rm {F}}(a,b)\equiv c_{-}(a,b).

Relation to hyperbolic functions

c_{\eta }(a,b)={\frac {\sinh \beta b}{2b(\cosh \beta a-\eta \cosh \beta b)}}.

It is obvious that $c_{\rm {F}}(a,b)$ is positive definite.

To avoid overflow in the numerical calculation, the tanh and coth functions are used

c_{\rm {B}}(a,b)={\frac {1}{4b}}\left(\operatorname {coth} {\frac {\beta (a-b)}{2}}-\operatorname {coth} {\frac {\beta (a+b)}{2}}\right),

c_{\rm {F}}(a,b)={\frac {1}{4b}}\left(\operatorname {tanh} {\frac {\beta (a+b)}{2}}-\operatorname {tanh} {\frac {\beta (a-b)}{2}}\right).

Case a = 0

c_{\rm {B}}(0,b)=-{\frac {1}{2b}}\operatorname {coth} {\frac {\beta b}{2}},

c_{\rm {F}}(0,b)={\frac {1}{2b}}\operatorname {tanh} {\frac {\beta b}{2}}.

Case b = 0

c_{\rm {B}}(a,0)={\frac {\beta }{4}}\operatorname {csch} ^{2}{\frac {\beta a}{2}},

c_{\rm {F}}(a,0)={\frac {\beta }{4}}\operatorname {sech} ^{2}{\frac {\beta a}{2}}.

Low temperature limit

For a = 0: $c_{\rm {F}}(0,b)={\frac {1}{2|b|}}.$

For b = 0: $c_{\rm {F}}(a,0)=\delta (a).$

In general,

c_{\rm {F}}(a,b)={\begin{cases}{\frac {1}{2|b|}},&{\text{if }}|a|<|b|\\0,&{\text{if }}|a|>|b|\end{cases}}

External links

Agustin Nieto: Evaluating Sums over the Matsubara Frequencies. arXiv:hep-ph/9311210

Github repository: MatsubaraSum A Mathematica package for Matsubara frequency summation.

A. Taheridehkordi, S. Curnoe, J.P.F. LeBlanc: Algorithmic Matsubara Integration for Hubbard-like models.. arXiv:cond-mat/1808.05188

References

↑ A. Abrikosov, L. Gor'kov, I. Dzyaloshinskii: Methods of Quantum Field Theory in Statistical Physics., New York, Dover Publ., 1975, ISBN 0-486-63228-8
↑ [Piers Coleman]: Introduction to Many-Body Physics., Cambridge University Press., 2015, ISBN 978-0-521-86488-6
1 2 Mahan, Gerald D. (2000). Many-particle physics (3rd ed.). New York: Kluwer Academic/Plenum Publishers. ISBN 0-306-46338-5. OCLC 43864386.
↑ Summation of series: Sommerfeld-Watson transformation, Lecture notes, M. G. Rozman

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] A. Abrikosov, L. Gor'kov, I. Dzyaloshinskii: Methods of Quantum Field Theory in Statistical Physics., New York, Dover Publ., 1975, ISBN 0-486-63228-8

[2] [Piers Coleman]: Introduction to Many-Body Physics., Cambridge University Press., 2015, ISBN 978-0-521-86488-6

[:0-3] 1 2 Mahan, Gerald D. (2000). Many-particle physics (3rd ed.). New York: Kluwer Academic/Plenum Publishers. ISBN 0-306-46338-5. OCLC 43864386.

[4] Summation of series: Sommerfeld-Watson transformation, Lecture notes, M. G. Rozman

[1]

[2]

[3]

[4]

Summation formalism

General formalism

Choice of Matsubara weighting function

Table of Matsubara frequency summations

Applications in physics

Zero temperature limit

Green's function related

Time domain

Operator switching effect

Distribution function

Free energy

Diagram evaluations

Fermion self energy

Particle-hole bubble

Particle-particle bubble

Appendix: Properties of distribution functions

Distribution functions

Relation to hyperbolic functions

Parity

Bose–Fermi transmutation

Derivatives

First order

Second order

Formula of difference

Case a = 0

Case a → 0

Case b → 0

The function cη

Relation to hyperbolic functions

Case a = 0

Case b = 0

Low temperature limit

See also

External links

References

The function c_η