Midpoint theorem (triangle)

{\begin{aligned}&{\text{D and E midpoints of AC and BC}}\\\Rightarrow \,&DE\parallel AB{\text{ and }}2|DE|=|AB|\end{aligned}}

The midpoint theorem or midline theorem states that if the midpoints of two sides of a triangle are connected, then the resulting line segment will be parallel to the third side and have half of its length. The midpoint theorem generalizes to the intercept theorem, where rather than using midpoints, both sides are partioned in the same ratio.

The converse of the theorem is true as well. That is if a line is drawn through the midpoint of triangle side parallel to another triangle side then the line will bisect the third side of the triangle.

The triangle formed by the three parallel lines through the three midpoints of sides of a triangle is called its medial triangle.

Proof

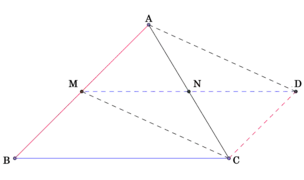Given: In a $\triangle ABC$ the points M and N are the midpoints of the sides AB and AC respectively. Construction: MN extended to D where MN=DN, join C to D. To Prove: $MN\parallel BC$ $MN={1 \over 2}BC$ Proof: $AN=CN$ (given) $\angle ANM=\angle CND$ (vertically opposite angle) $MN=DN$ (constructible) Hence by Side angle side. $\triangle AMN\cong \triangle CDN$ Therefore, the corresponding sides and angles of congruent triangles are equal $AM=BM=CD$ $\angle MAN=\angle DCN$ Transversal AC intersects the lines AB and CD and alternate angles ∠MAN and ∠DCN are equal. Therefore $AM\parallel CD\parallel BM$ Hence BCDM is a parallelogram. BC and DM are also equal and parallel. $MN\parallel BC$ $MN={1 \over 2}MD={1 \over 2}BC$

References

French, Doug (2004). Teaching and Learning Geometry. Bloomsbury. pp. 81–84. ISBN 9780826473622. (online copy, p. 81, at Google Books)
Clapham, Christopher; Nicholson, James (2009). The Concise Oxford Dictionary of Mathematics. Oxford University Press. p. 297. ISBN 9780199235940. (online copy, p. 297, at Google Books)

External links

The midpoint theorem and its converse
The Mid-Point Theorem
Midpoint theorem and converse Euclidean explained Grade 10+12 (video, 5:28 mins)
midpoint theorem at the Proof Wiki

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.