In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph.^[1] If the graph does not contain any cycles (that is, it is a forest), its girth is defined to be infinity.^[2] For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.

Cages

A cubic graph (all vertices have degree three) of girth g that is as small as possible is known as a g-cage (or as a (3,g)-cage). The Petersen graph is the unique 5-cage (it is the smallest cubic graph of girth 5), the Heawood graph is the unique 6-cage, the McGee graph is the unique 7-cage and the Tutte eight cage is the unique 8-cage.^[3] There may exist multiple cages for a given girth. For instance there are three nonisomorphic 10-cages, each with 70 vertices: the Balaban 10-cage, the Harries graph and the Harries–Wong graph.

• 
  The Petersen graph has a girth of 5
• 
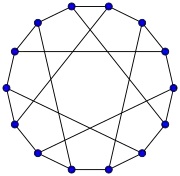  The Heawood graph has a girth of 6
• 
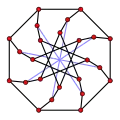  The McGee graph has a girth of 7
• 
  The Tutte–Coxeter graph (Tutte eight cage) has a girth of 8

Girth and graph coloring

For any positive integers g and χ, there exists a graph with girth at least g and chromatic number at least χ; for instance, the Grötzsch graph is triangle-free and has chromatic number 4, and repeating the Mycielskian construction used to form the Grötzsch graph produces triangle-free graphs of arbitrarily large chromatic number. Paul Erdős was the first to prove the general result, using the probabilistic method.^[4] More precisely, he showed that a random graph on n vertices, formed by choosing independently whether to include each edge with probability n^(1–g)/g, has, with probability tending to 1 as n goes to infinity, at most n⁄2 cycles of length g or less, but has no independent set of size n⁄2k . Therefore, removing one vertex from each short cycle leaves a smaller graph with girth greater than g, in which each color class of a coloring must be small and which therefore requires at least k colors in any coloring.

Explicit, though large, graphs with high girth and chromatic number can be constructed as certain Cayley graphs of linear groups over finite fields.^[5] These remarkable Ramanujan graphs also have large expansion coefficient.

Related concepts

The odd girth and even girth of a graph are the lengths of a shortest odd cycle and shortest even cycle respectively.

The circumference of a graph is the length of the longest (simple) cycle, rather than the shortest.

Thought of as the least length of a non-trivial cycle, the girth admits natural generalisations as the 1-systole or higher systoles in systolic geometry.

Girth is the dual concept to edge connectivity, in the sense that the girth of a planar graph is the edge connectivity of its dual graph, and vice versa. These concepts are unified in matroid theory by the girth of a matroid, the size of the smallest dependent set in the matroid. For a graphic matroid, the matroid girth equals the girth of the underlying graph, while for a co-graphic matroid it equals the edge connectivity.^[6]

Computation

The girth of an undirected graph can be computed by running a breadth-first search from each node, with complexity ${\displaystyle O(nm)}$ where ${\displaystyle n}$ is the number of vertices of the graph and ${\displaystyle m}$ is the number of edges.^[7] A practical optimization is to limit the depth of the BFS to a depth that depends on the length of the smallest cycle discovered so far.^[8] Better algorithms are known in the case where the girth is even^[9] and when the graph is planar.^[10] In terms of lower bounds, computing the girth of a graph is at least as hard as solving the triangle finding problem on the graph.

References