In mathematics, persymmetric matrix may refer to:

1. a square matrix which is symmetric with respect to the northeast-to-southwest diagonal (anti-diagonal); or
2. a square matrix such that the values on each line perpendicular to the main diagonal are the same for a given line.

The first definition is the most common in the recent literature. The designation "Hankel matrix" is often used for matrices satisfying the property in the second definition.

Definition 1

Symmetry pattern of a persymmetric 5 × 5 matrix

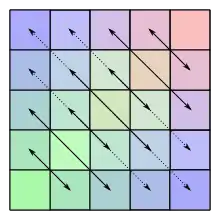
Let A = (a_ij) be an n × n matrix. The first definition of persymmetric requires that

${\displaystyle a_{ij}=a_{n-j+1,\,n-i+1}}$ for all i, j.^[1]

For example, 5 × 5 persymmetric matrices are of the form

${\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&a_{13}&a_{14}&a_{15}\\a_{21}&a_{22}&a_{23}&a_{24}&a_{14}\\a_{31}&a_{32}&a_{33}&a_{23}&a_{13}\\a_{41}&a_{42}&a_{32}&a_{22}&a_{12}\\a_{51}&a_{41}&a_{31}&a_{21}&a_{11}\end{bmatrix}}.}$

This can be equivalently expressed as AJ = JA^T where J is the exchange matrix.

A third way to express this is seen by post-multiplying AJ = JA^T with J on both sides, showing that A^T rotated 180 degrees is identical to A:

${\displaystyle A=JA^{\mathsf {T}}J.}$

A symmetric matrix is a matrix whose values are symmetric in the northwest-to-southeast diagonal. If a symmetric matrix is rotated by 90°, it becomes a persymmetric matrix. Symmetric persymmetric matrices are sometimes called bisymmetric matrices.

Definition 2

The second definition is due to Thomas Muir.^[2] It says that the square matrix A = (a_ij) is persymmetric if a_ij depends only on i + j. Persymmetric matrices in this sense, or Hankel matrices as they are often called, are of the form

${\displaystyle A={\begin{bmatrix}r_{1}&r_{2}&r_{3}&\cdots &r_{n}\\r_{2}&r_{3}&r_{4}&\cdots &r_{n+1}\\r_{3}&r_{4}&r_{5}&\cdots &r_{n+2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\r_{n}&r_{n+1}&r_{n+2}&\cdots &r_{2n-1}\end{bmatrix}}.}$

A persymmetric determinant is the determinant of a persymmetric matrix.^[2]

A matrix for which the values on each line parallel to the main diagonal are constant is called a Toeplitz matrix.

See also

• Centrosymmetric matrix

References