The Petrie polygon of the dodecahedron is a skew decagon. Seen from the solid's 5-fold symmetry axis it looks like a regular decagon. Every pair of consecutive sides belongs to one pentagon (but no triple does).

In topological graph theory, the Petrie dual of an embedded graph (on a 2-manifold with all faces disks) is another embedded graph that has the Petrie polygons of the first embedding as its faces.^[1]

The Petrie dual is also called the Petrial, and the Petrie dual of an embedded graph ${\displaystyle G}$ may be denoted ${\displaystyle G^{\pi }}$.^[2] It can be obtained from a signed rotation system or ribbon graph representation of the embedding by twisting every edge of the embedding.

Properties

Like the usual dual graph, repeating the Petrie dual operation twice returns to the original surface embedding. Unlike the usual dual graph (which is an embedding of a generally different graph in the same surface) the Petrie dual is an embedding of the same graph in a generally different surface.^[1]

Surface duality and Petrie duality are two of the six Wilson operations, and together generate the group of these operations.^[3]

Regular polyhedra

Applying the Petrie dual to a regular polyhedron produces a regular map.^[2] The number of skew h-gonal faces is g/2h, where g is the group order, and h is the coxeter number of the group.

For example, the Petrie dual of a cube (a bipartite graph with eight vertices and twelve edges, embedded onto a sphere with six square faces) has four^[4] hexagonal faces, the equators of the cube. Topologically, it forms an embedding of the same graph onto a torus.^[1]

The regular maps obtained in this way are as follows.

• The petrial tetrahedron, {3,3}^π, has 4 vertices, 6 edges, and 3 skew square faces. With an Euler characteristic, χ, of 1, it is topologically identical to the hemi-cube, {4,3}/2.
• The petrial cube, {4,3}^π, has 8 vertices, 12 edges, and 4 skew hexagons, colored red, green, blue and orange here. With an Euler characteristic of 0, it can also be seen in the four hexagonal faces of the hexagonal tiling as type {6,3}_(2,0).
• The petrial octahedron, {3,4}^π, has 6 vertices, 12 edges, and 4 skew hexagon faces. It has an Euler characteristic of −2, and has a mapping to the hyperbolic order-4 hexagonal tiling, as type {6,4}₃.
• The petrial dodecahedron, {5,3}^π, has 20 vertices, 30 edges, and 6 skew decagonal faces, and Euler characteristic of −4, related to the hyperbolic tiling as type {10,3}₅.
• The petrial icosahedron, {3,5}^π, has 12 vertices, 30 edges, and 6 skew decagonal faces, and Euler characteristic of −12, related to the hyperbolic tiling as type {10,5}₃.

Regular petrials

Name	Petrial tetrahedron	Petrial cube	Petrial octahedron	Petrial dodecahedron	Petrial icosahedron
Symbol	{3,3}π , {4,3}3	{4,3}π , {6,3}4	{3,4}π , {6,4}3	{5,3}π , {10,3}	{3,5}π , {10,5}
(v,e,f), χ	(4,6,3), χ = 1	(8,12,4), χ = 0	(6,12,4), χ = −2	(20,30,6), χ = −4	(12,30,6), χ = −12
Faces	3 skew squares	4 skew hexagons		6 skew decagons
Image
Animation
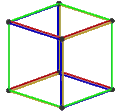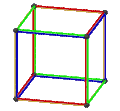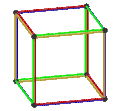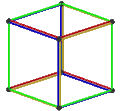Related figures	{4,3}3 = {4,3}/2 = {4,3}(2,0)	{6,3}3 = {6,3}(2,0)	{6,4}3 = {6,4}(4,0)	{10,3}5	{10,5}3

There are also 4 petrials of the Kepler–Poinsot polyhedra:

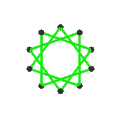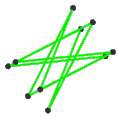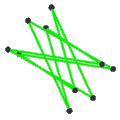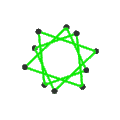
• The petrial great dodecahedron, {5,5/2}^π, has 12 vertices, 30 edges, and 10 skew hexagon faces with an Euler characteristic, χ, of -8.
• The petrial small stellated dodecahedron, {5/2,5}^π, has 12 vertices, 30 edges, and 10 skew hexagon faces with χ of -8.
• The petrial great icosahedron, {3,5/2}^π, has 12 vertices, 30 edges, and 6 skew decagram faces with χ of -12.
• The petrial great stellated dodecahedron, {5/2,3}^π, has 20 vertices, 30 edges, and 6 skew decagram faces with χ of -4.

Regular star petrials

Name	Petrial great dodecahedron	Petrial small stellated dodecahedron	Petrial great icosahedron	Petrial great stellated dodecahedron
Symbol	{5,5/2}π , {6,5/2}	{5/2,5}π , {6,5}	{3,5/2}π , {10/3,5/2}	{5/2,3}π , {10/3,3}
(v,e,f), χ	(12,30,10), χ = -8	(12,30,10), χ = -8	(12,30,6), χ = -12	(20,30,6), χ = -4
Faces	10 skew hexagons		6 skew decagrams (one blue decagram outlined)
Image
Animation

References