Variation in the Prandtl–Meyer function (${\displaystyle \nu }$) with Mach number (${\displaystyle M}$) and ratio of specific heat capacity (${\displaystyle \gamma }$). The dashed lines show the limiting value ${\displaystyle \nu _{\text{max}}}$ as Mach number tends to infinity.

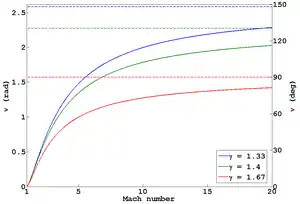
In aerodynamics, the Prandtl–Meyer function describes the angle through which a flow turns isentropically from sonic velocity (M=1) to a Mach (M) number greater than 1. The maximum angle through which a sonic (M = 1) flow can be turned around a convex corner is calculated for M = ${\displaystyle \infty }$. For an ideal gas, it is expressed as follows,

${\displaystyle {\begin{aligned}\nu (M)&=\int {\frac {\sqrt {M^{2}-1}}{1+{\frac {\gamma -1}{2}}M^{2}}}{\frac {\,dM}{M}}\\[4pt]&={\sqrt {\frac {\gamma +1}{\gamma -1}}}\cdot \arctan {\sqrt {{\frac {\gamma -1}{\gamma +1}}(M^{2}-1)}}-\arctan {\sqrt {M^{2}-1}}\end{aligned}}}$

where ${\displaystyle \nu \,}$ is the Prandtl–Meyer function, ${\displaystyle M}$ is the Mach number of the flow and ${\displaystyle \gamma }$ is the ratio of the specific heat capacities.

By convention, the constant of integration is selected such that ${\displaystyle \nu (1)=0.\,}$

As Mach number varies from 1 to ${\displaystyle \infty }$, ${\displaystyle \nu \,}$ takes values from 0 to ${\displaystyle \nu _{\text{max}}\,}$, where

${\displaystyle \nu _{\text{max}}={\frac {\pi }{2}}{\bigg (}{\sqrt {\frac {\gamma +1}{\gamma -1}}}-1{\bigg )}}$

For isentropic expansion,	${\displaystyle \nu (M_{2})=\nu (M_{1})+\theta \,}$
For isentropic compression,	${\displaystyle \nu (M_{2})=\nu (M_{1})-\theta \,}$

where, ${\displaystyle \theta }$ is the absolute value of the angle through which the flow turns, ${\displaystyle M}$ is the flow Mach number and the suffixes "1" and "2" denote the initial and final conditions respectively.

See also

• Gas dynamics
• Prandtl–Meyer expansion fan

References

• Liepmann, Hans W.; Roshko, A. (2001) [1957]. Elements of Gasdynamics. Dover Publications. ISBN 978-0-486-41963-3.