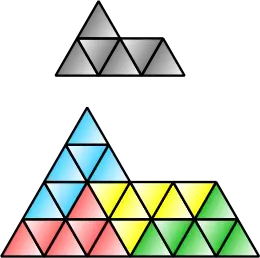
The "sphinx" polyiamond rep-tile. Four copies of the sphinx can be put together as shown to make a larger sphinx.

In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American.[1] In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.[2]

A selection of rep-tiles, including the sphinx, two fish and the 5-triangle

Terminology

The chair substitution (left) and a portion of a chair tiling (right)

A rep-tile is labelled rep-n if the dissection uses n copies. Such a shape necessarily forms the prototile for a tiling of the plane, in many cases an aperiodic tiling. A rep-tile dissection using different sizes of the original shape is called an irregular rep-tile or irreptile. If the dissection uses n copies, the shape is said to be irrep-n. If all these sub-tiles are of different sizes then the tiling is additionally described as perfect. A shape that is rep-n or irrep-n is trivially also irrep-(kn − k + n) for any k > 1, by replacing the smallest tile in the rep-n dissection by n even smaller tiles. The order of a shape, whether using rep-tiles or irrep-tiles is the smallest possible number of tiles which will suffice.[3]

Examples

Defining an aperiodic tiling (the pinwheel tiling) by repeatedly dissecting and inflating a rep-tile.

Every square, rectangle, parallelogram, rhombus, or triangle is rep-4. The sphinx hexiamond (illustrated above) is rep-4 and rep-9, and is one of few known self-replicating pentagons. The Gosper island is rep-7. The Koch snowflake is irrep-7: six small snowflakes of the same size, together with another snowflake with three times the area of the smaller ones, can combine to form a single larger snowflake.

A right triangle with side lengths in the ratio 1:2 is rep-5, and its rep-5 dissection forms the basis of the aperiodic pinwheel tiling. By Pythagoras' theorem, the hypotenuse, or sloping side of the rep-5 triangle, has a length of √5.

The international standard ISO 216 defines sizes of paper sheets using the √2, in which the long side of a rectangular sheet of paper is the square root of two times the short side of the paper. Rectangles in this shape are rep-2. A rectangle (or parallelogram) is rep-n if its aspect ratio is √n:1. An isosceles right triangle is also rep-2.

Rep-tiles and symmetry

Some rep-tiles, like the square and equilateral triangle, are symmetrical and remain identical when reflected in a mirror. Others, like the sphinx, are asymmetrical and exist in two distinct forms related by mirror-reflection. Dissection of the sphinx and some other asymmetric rep-tiles requires use of both the original shape and its mirror-image.

Rep-tiles and polyforms

Some rep-tiles are based on polyforms like polyiamonds and polyominoes, or shapes created by laying equilateral triangles and squares edge-to-edge.

Squares

If a polyomino is rectifiable, that is, able to tile a rectangle, then it will also be a rep-tile, because the rectangle will have an integer side length ratio and will thus tile a square. This can be seen in the octominoes, which are created from eight squares. Two copies of some octominoes will tile a square; therefore these octominoes are also rep-16 rep-tiles.

Rep-tiles based on rectifiable octominoes

Four copies of some nonominoes and nonakings will tile a square, therefore these polyforms are also rep-36 rep-tiles.

Rep-tiles created from rectifiable nonominoes and 9-polykings (nonakings)

Equilateral triangles

Similarly, if a polyiamond tiles an equilateral triangle, it will also be a rep-tile.

Rep-tiles created from equilateral triangles


A fish-like rep-tile based on three equilateral triangles
A rocket-like rep-tile created from a dodeciamond, or twelve equilateral triangles laid edge-to-edge (and corner-to-corner)

Right triangles

A right triangle is a triangle containing one right angle of 90°. Two particular forms of right triangle have attracted the attention of rep-tile researchers, the 45°-90°-45° triangle and the 30°-60°-90° triangle.

45°-90°-45° triangles

Polyforms based on isosceles right triangles, with sides in the ratio 1 : 1 : √2, are known as polyabolos. An infinite number of them are rep-tiles. Indeed, the simplest of all rep-tiles is a single isosceles right triangle. It is rep-2 when divided by a single line bisecting the right angle to the hypotenuse. Rep-2 rep-tiles are also rep-2n and the rep-4,8,16+ triangles yield further rep-tiles. These are found by discarding half of the sub-copies and permutating the remainder until they are mirror-symmetrical within a right triangle. In other words, two copies will tile a right triangle. One of these new rep-tiles is reminiscent of the fish formed from three equilateral triangles.

Rep-tiles based on right triangles
A fish-like rep-tile based on four isosceles right triangles

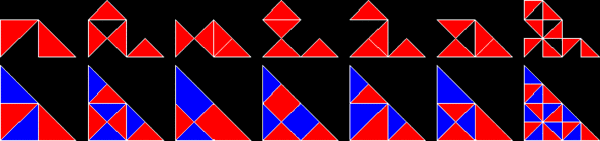
30°-60°-90° triangles

Polyforms based on 30°-60°-90° right triangles, with sides in the ratio 1 : √3 : 2, are known as polydrafters. Some are identical to polyminoes and polyiamonds, others are distinct.[4]

Ένα τρισδιάστατο, ή σχήμα που δημιουργείται από τρία τρίγωνα 30-60-90°.
Ο tridrafter ως reptile.
Ένα tetradrafter, ή σχήμα που δημιουργείται από τέσσερα τρίγωνα 30-60-90°.
Ο tetradrafter ως reptile
Ένα hexadrafter, ή σχήμα που δημιουργείται από έξι τρίγωνα 30-60-90°.
Ο hexadrafter ως reptile.

Multiple and variant rep-tilings

Many of the common rep-tiles are rep-n2 for all positive integer values of n. In particular this is true for three trapezoids including the one formed from three equilateral triangles, for three axis-parallel hexagons (the L-tromino, L-tetromino, and P-pentomino), and the sphinx hexiamond.[5] In addition, many rep-tiles, particularly those with higher rep-n, can be self-tiled in different ways. For example, the rep-9 L-tetramino has at least fourteen different rep-tilings. The rep-9 sphinx hexiamond can also be tiled in different ways.

Variant rep-tilings of the rep-9 L-tetromino
Variant rep-tilings of the rep-9 sphinx hexiamond

Rep-tiles with infinite sides

Horned triangle or teragonic triangle

The most familiar rep-tiles are polygons with a finite number of sides, but some shapes with an infinite number of sides can also be rep-tiles. For example, the teragonic triangle, or horned triangle, is rep-4. It is also an example of a fractal rep-tile.

Pentagonal rep-tiles

Triangular and quadrilateral (four-sided) rep-tiles are common, but pentagonal rep-tiles are rare. For a long time, the sphinx was widely believed to be the only example known, but the German/New-Zealand mathematician Karl Scherer and the American mathematician George Sicherman have found more examples, including a double-pyramid and an elongated version of the sphinx. These pentagonal rep-tiles are illustrated on the Math Magic pages overseen by the American mathematician Erich Friedman.[6] However, the sphinx and its extended versions are the only known pentagons that can be rep-tiled with equal copies. See Clarke's Reptile pages.

A pentagonal rep-tile discovered by Karl Scherer

Rep-tiles and fractals

Rep-tiles as fractals

Rep-tiles can be used to create fractals, or shapes that are self-similar at smaller and smaller scales. A rep-tile fractal is formed by subdividing the rep-tile, removing one or more copies of the subdivided shape, and then continuing recursively. For instance, the Sierpinski carpet is formed in this way from a rep-tiling of a square into 27 smaller squares, and the Sierpinski triangle is formed from a rep-tiling of an equilateral triangle into four smaller triangles. When one sub-copy is discarded, a rep-4 L-triomino can be used to create four fractals, two of which are identical except for orientation.

Geometrical dissection of an L-triomino (rep-4)
A fractal based on an L-triomino (rep-4)
Another fractal based on an L-triomino
Another fractal based on an L-triomino

Fractals as rep-tiles

Because fractals are often self-similar on smaller and smaller scales, many may be decomposed into copies of themselves like a rep-tile. However, if the fractal has an empty interior, this decomposition may not lead to a tiling of the entire plane. For example, the Sierpinski triangle is rep-3, tiled with three copies of itself, and the Sierpinski carpet is rep-8, tiled with eight copies of itself, but repetition of these decompositions does not form a tiling. On the other hand, the dragon curve is a space-filling curve with a non-empty interior; it is rep-4, and does form a tiling. Similarly, the Gosper island is rep-7, formed from the space-filling Gosper curve, and again forms a tiling.

By construction, any fractal defined by an iterated function system of n contracting maps of the same ratio is rep-n.

A Sierpinski triangle based on three smaller copies of a Sierpinski triangle
A Sierpinski carpet based on eight smaller copies of a Sierpinski carpet
A dragon curve based on 4 smaller copies of a dragon curve

Infinite tiling

Among regular polygons, only the triangle and square can be dissected into smaller equally sized copies of themselves. However, a regular hexagon can be dissected into six equilateral triangles, each of which can be dissected into a regular hexagon and three more equilateral triangles. This is the basis for an infinite tiling of the hexagon with hexagons. The hexagon is therefore an irrep-∞ or irrep-infinity irreptile.


See also

Notes

  1. ↑ A Gardner's Dozen—Martin's Scientific American Cover Stories
  2. ↑ Sallows (2012).
  3. ↑ Gardner (2001).
  4. ↑ Polydrafter Irreptiling
  5. ↑ Niţică (2003).
  6. ↑ Math Magic, Problem of the Month (October 2002)
  7. ↑ Pietrocola, Giorgio (2005). "Tartapelago. Arte tassellazione". Maecla.

References

  • Gardner, M. (2001), "Rep-Tiles", The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, New York: W. W. Norton, pp. 46–58
  • Gardner, M. (1991), "Chapter 19: Rep-Tiles, Replicating Figures on the Plane", The Unexpected Hanging and Other Mathematical Diversions, Chicago, IL: Chicago University Press, pp. 222–233
  • Langford, C. D. (1940), "Uses of a Geometric Puzzle", The Mathematical Gazette, 24 (260): 209–211, doi:10.2307/3605717
  • Niţică, Viorel (2003), "Rep-tiles revisited", MASS selecta, Providence, RI: American Mathematical Society, pp. 205–217, MR 2027179
  • Sallows, Lee (2012), "On self-tiling tile sets", Mathematics Magazine, 85 (5): 323–333, doi:10.4169/math.mag.85.5.323, MR 3007213
  • Scherer, Karl (1987), A Puzzling Journey to the Reptiles and Related Animals
  • Wells, D. (1991), The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin, pp. 213–214

Rep-tiles

Wikimedia Commons has media related to Rep-tiles.

Irrep-tiles

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.