Classic model used for deriving the equations of a mass spring damper model

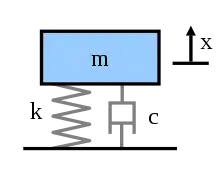
The mass-spring-damper model consists of discrete mass nodes distributed throughout an object and interconnected via a network of springs and dampers. This model is well-suited for modelling object with complex material properties such as nonlinearity and viscoelasticity. Packages such as MATLAB may be used to run simulations of such models.^[1] As well as engineering simulation, these systems have applications in computer graphics and computer animation.^[2]

Derivation (Single Mass)

Deriving the equations of motion for this model is usually done by examining the sum of forces on the mass:

${\displaystyle \Sigma F=-kx-c{\dot {x}}+F_{external}=m{\ddot {x}}}$

By rearranging this equation, we can derive the standard form:

${\displaystyle {\ddot {x}}+2\zeta \omega _{n}{\dot {x}}+\omega _{n}^{2}x=u}$ where ${\displaystyle \omega _{n}={\sqrt {\frac {k}{m}}};\quad \zeta ={\frac {c}{2m\omega _{n}}};\quad u={\frac {F_{\text{external}}}{m}}}$

${\displaystyle \omega _{n}}$ is the undamped natural frequency and ${\displaystyle \zeta }$ is the damping ratio. The homogeneous equation for the mass spring system is:

${\displaystyle {\ddot {x}}+2\zeta \omega _{n}{\dot {x}}+\omega _{n}^{2}x=0}$

This has the solution:

${\displaystyle x=Ae^{-\omega _{n}t\left(\zeta +{\sqrt {\zeta ^{2}-1}}\right)}+Be^{-\omega _{n}t\left(\zeta -{\sqrt {\zeta ^{2}-1}}\right)}}$

If ${\displaystyle \zeta <1}$ then ${\displaystyle \zeta ^{2}-1}$ is negative, meaning the square root will be negative the solution will have an oscillatory component.

See also

• Numerical methods
• Soft body dynamics#Spring/mass models
• Finite element analysis

References