Trapezo-rhombic dodecahedron
TypePlesiohedron
Johnson solid dual
Faces6 rhombi
6 trapezoids
Edges24
Vertices14
Vertex configuration(2) 4.4.4
(6) 4.4.4.4
(6) 4.4.4
Symmetry groupD3h, [3,2], (*322), order 12
Rotation groupD3, [3,2]+, (322), order 6
Dual polyhedronTriangular orthobicupola
Propertiesconvex
Net
Concave configuration
Concave configuration

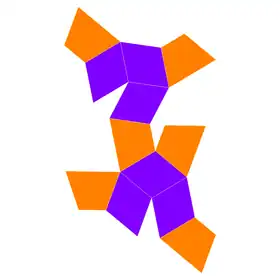In geometry, the trapezo-rhombic dodecahedron or rhombo-trapezoidal dodecahedron is a convex dodecahedron with 6 rhombic and 6 trapezoidal faces. It has D3h symmetry. A concave form can be constructed with an identical net, seen as excavating trigonal trapezohedra from the top and bottom. It is also called the trapezoidal dodecahedron.[1]

Construction

This polyhedron could be constructed by taking a tall uniform hexagonal prism, and making 3 angled cuts on the top and bottom. The trapezoids represent what remains of the original prism sides, and the 6 rhombi a result of the top and bottom cuts.

Space-filling tessellation

A space-filling tessellation, the trapezo-rhombic dodecahedral honeycomb, can be made by translated copies of this cell. Each "layer" is a hexagonal tiling, or a rhombille tiling, and alternate layers are connected by shifting their centers and rotating each polyhedron so the rhombic faces match up.

:

In the special case that the long sides of the trapezoids equals twice the length of the short sides, the solid now represents the 3D Voronoi cell of a sphere in a hexagonal close packing, next to face-centered cubic an optimal way to stack spheres in a lattice. It is therefore related to the rhombic dodecahedron, which can be represented by turning the lower half of the picture at right over an angle of 60 degrees. The rhombic dodecahedron is a Voronoi cell of the other optimal way to stack spheres. The two shapes differ in their combinatorial structure as well as in their geometry: in the rhombic dodecahedron, every edge connects a degree-three vertex to a degree-four vertex, whereas the trapezo-rhombic dodecahedron has six edges that connect vertices of equal degrees.

As the Voronoi cell of a regular space pattern, it is a plesiohedron. It is the polyhedral dual of the triangular orthobicupola.

Variations

The trapezo-rhombic dodecahedron can be seen as an elongation of another dodecahedron, which can be called a rhombo-triangular dodecahedron, with 6 rhombi (or squares) and 6 triangles. It also has d3h symmetry and is space-filling. It has 21 edges and 11 vertices. With square faces it can be seen as a cube split across the 3-fold axis, separated with the two halves rotated 180 degrees, and filling the gaps with triangles. When used as a space-filler, connecting dodecahedra on their triangles leaves two cubical step surfaces on the top and bottom which can connect with complementary steps.

See also

References

  1. ↑ Lagarias, Jeffrey C. (2011). "The Kepler conjecture and its proof". The Kepler Conjecture: The Hales–Ferguson proof. Springer, New York. pp. 3–26. doi:10.1007/978-1-4614-1129-1_1. MR 3050907.; see especially p. 11

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.