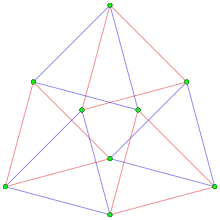
In geometry of 4 dimensions or higher, a proprism is a polytope resulting from the Cartesian product of two or more polytopes, each of two dimensions or higher. The term was coined by John Horton Conway for product prism. The dimension of the space of a proprism equals the sum of the dimensions of all its product elements. Proprisms are often seen as k-face elements of uniform polytopes.[1]
Properties
The number of vertices in a proprism is equal to the product of the number of vertices in all the polytopes in the product.
The minimum symmetry order of a proprism is the product of the symmetry orders of all the polytopes. A higher symmetry order is possible if polytopes in the product are identical.
A proprism is convex if all its product polytopes are convex.
f-vectors
An f-vector is a number of k-face elements in a polytope from k=0 (points) to k=n-1 (facets). An extended f-vector can also include k=-1 (nullitope), or k=n (body). Prism products include the body element. (The dual to prism products includes the nullitope, while pyramid products include both.)
The f-vector of prism product, A×B, can be computed as (fA,1)*(fB,1), like polynomial multiplication polynomial coefficients.
For example for product of a triangle, f=(3,3), and dion, f=(2) makes a triangular prism with 6 vertices, 9 edges, and 5 faces:
- fA(x) = (3,3,1) = 3 + 3x + x2 (triangle)
- fB(x) = (2,1) = 2 + x (dion)
- fA∨B(x) = fA(x) * fB(x)
- = (3 + 3x + x2) * (2 + x)
- = 6 + 9x + 5x2 + x3
- = (6,9,5,1)
Hypercube f-vectors can be computed as Cartesian products of n dions, { }n. Each { } has f=(2), extended to f=(2,1).
For example, an 8-cube will have extended f-vector power product: f=(2,1)8 = (4,4,1)4 = (16,32,24,8,1)2 = (256,1024,1792,1792,1120,448,112,16,1). If equal lengths, this doubling represents { }8, a square tetra-prism {4}4, a tesseract duo-prism {4,3,3}2, and regular 8-cube {4,3,3,3,3,3,3}.
Double products or duoprisms
In geometry of 4 dimensions or higher, duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an a-polytope, a b-polytope is an (a+b)-polytope, where a and b are 2-polytopes (polygon) or higher.
Most commonly this refers to the product of two polygons in 4-dimensions. In the context of a product of polygons, Henry P. Manning's 1910 work explaining the fourth dimension called these double prisms.[2]
The Cartesian product of two polygons is the set of points:
where P1 and P2 are the sets of the points contained in the respective polygons.
The smallest is a 3-3 duoprism, made as the product of 2 triangles. If the triangles are regular it can be written as a product of Schläfli symbols, {3} × {3}, and is composed of 9 vertices.
The tesseract, can be constructed as the duoprism {4} × {4}, the product of two equal-size orthogonal squares, composed of 16 vertices. The 5-cube can be constructed as a duoprism {4} × {4,3}, the product of a square and cube, while the 6-cube can be constructed as the product of two cubes, {4,3} × {4,3}.
Triple products
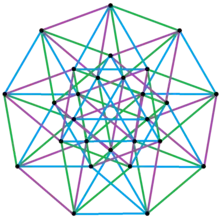
In geometry of 6 dimensions or higher, a triple product is a polytope resulting from the Cartesian product of three polytopes, each of two dimensions or higher. The Cartesian product of an a-polytope, a b-polytope, and a c-polytope is an (a + b + c)-polytope, where a, b and c are 2-polytopes (polygon) or higher.
The lowest-dimensional forms are 6-polytopes being the Cartesian product of three polygons. The smallest can be written as {3} × {3} × {3} in Schläfli symbols if they are regular, and contains 27 vertices. This is the product of three equilateral triangles and is a uniform polytope. The f-vectors can be computed by (3,3,1)3 = (27,81,108,81,36,9,1).
The 6-cube, can be constructed as a triple product {4} × {4} × {4}. The f-vectors can be computed by (4,4,1)3 = (64,192,240,160,60,12,1).
References
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26, p. 391 "proprism")
- ↑ The Fourth Dimension Simply Explained, Henry P. Manning, Munn & Company, 1910, New York. Available from the University of Virginia library. Also accessible online: The Fourth Dimension Simply Explained—contains a description of duoprisms (double prisms) and duocylinders (double cylinders). Googlebook