Tschirnhausen cubic, case of a = 1

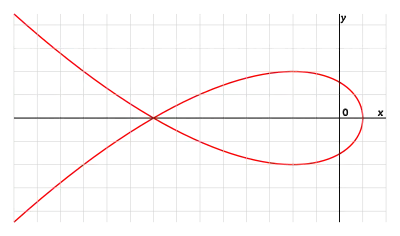
In algebraic geometry, the Tschirnhausen cubic, or Tschirnhaus' cubic is a plane curve defined, in its left-opening form, by the polar equation

${\displaystyle r=a\sec ^{3}\left({\frac {\theta }{3}}\right)}$

where sec is the secant function.

History

The curve was studied by von Tschirnhaus, de L'Hôpital, and Catalan. It was given the name Tschirnhausen cubic in a 1900 paper by Raymond Clare Archibald, though it is sometimes known as de L'Hôpital's cubic or the trisectrix of Catalan.

Other equations

Put ${\displaystyle t=\tan(\theta /3)}$. Then applying triple-angle formulas gives

${\displaystyle x=a\cos \theta \sec ^{3}{\frac {\theta }{3}}=a\left(\cos ^{3}{\frac {\theta }{3}}-3\cos {\frac {\theta }{3}}\sin ^{2}{\frac {\theta }{3}}\right)\sec ^{3}{\frac {\theta }{3}}=a\left(1-3\tan ^{2}{\frac {\theta }{3}}\right)}$

${\displaystyle =a(1-3t^{2})}$

${\displaystyle y=a\sin \theta \sec ^{3}{\frac {\theta }{3}}=a\left(3\cos ^{2}{\frac {\theta }{3}}\sin {\frac {\theta }{3}}-\sin ^{3}{\frac {\theta }{3}}\right)\sec ^{3}{\frac {\theta }{3}}=a\left(3\tan {\frac {\theta }{3}}-\tan ^{3}{\frac {\theta }{3}}\right)}$

${\displaystyle =at(3-t^{2})}$

giving a parametric form for the curve. The parameter t can be eliminated easily giving the Cartesian equation

${\displaystyle 27ay^{2}=(a-x)(8a+x)^{2}}$.

If the curve is translated horizontally by 8a and the signs of the variables are changed, the equations of the resulting right-opening curve are

${\displaystyle x=3a(3-t^{2})}$

${\displaystyle y=at(3-t^{2})}$

and in Cartesian coordinates

${\displaystyle x^{3}=9a\left(x^{2}-3y^{2}\right)}$.

This gives the alternative polar form

${\displaystyle r=9a\left(\sec \theta -3\sec \theta \tan ^{2}\theta \right)}$.

Generalization

The Tschirnhausen cubic is a Sinusoidal spiral with n = −1/3.

References

• J. D. Lawrence, A Catalog of Special Plane Curves. New York: Dover, 1972, pp. 87-90.

External links

• Weisstein, Eric W. "Tschirnhausen Cubic". MathWorld.
• "Tschirnhaus' Cubic" at MacTutor History of Mathematics archive
• Tschirnhausen cubic at mathcurve.com