List of integrals of inverse trigonometric functions

Trigonometry

Outline History Usage Functions (inverse) Generalized trigonometry
Reference
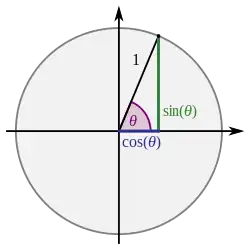Identities Exact constants Tables Unit circle
Laws and theorems
Sines Cosines Tangents Cotangents Pythagorean theorem
Calculus
Trigonometric substitution Integrals (inverse functions) Derivatives

The following is a list of indefinite integrals (antiderivatives) of expressions involving the inverse trigonometric functions. For a complete list of integral formulas, see lists of integrals.

The inverse trigonometric functions are also known as the "arc functions".
C is used for the arbitrary constant of integration that can only be determined if something about the value of the integral at some point is known. Thus each function has an infinite number of antiderivatives.
There are three common notations for inverse trigonometric functions. The arcsine function, for instance, could be written as sin⁻¹, asin, or, as is used on this page, arcsin.
For each inverse trigonometric integration formula below there is a corresponding formula in the list of integrals of inverse hyperbolic functions.

Arcsine function integration formulas

$\int \arcsin(x)\,dx=x\arcsin(x)+{\sqrt {1-x^{2}}}+C$
$\int \arcsin(ax)\,dx=x\arcsin(ax)+{\frac {\sqrt {1-a^{2}x^{2}}}{a}}+C$
$\int x\arcsin(ax)\,dx={\frac {x^{2}\arcsin(ax)}{2}}-{\frac {\arcsin(ax)}{4\,a^{2}}}+{\frac {x{\sqrt {1-a^{2}x^{2}}}}{4\,a}}+C$
$\int x^{2}\arcsin(ax)\,dx={\frac {x^{3}\arcsin(ax)}{3}}+{\frac {\left(a^{2}x^{2}+2\right){\sqrt {1-a^{2}x^{2}}}}{9\,a^{3}}}+C$
$\int x^{m}\arcsin(ax)\,dx={\frac {x^{m+1}\arcsin(ax)}{m+1}}\,-\,{\frac {a}{m+1}}\int {\frac {x^{m+1}}{\sqrt {1-a^{2}x^{2}}}}\,dx\,,\quad (m\neq -1)$
$\int \arcsin(ax)^{2}\,dx=-2x+x\arcsin(ax)^{2}+{\frac {2{\sqrt {1-a^{2}x^{2}}}\arcsin(ax)}{a}}+C$
$\int \arcsin(ax)^{n}\,dx=x\arcsin(ax)^{n}\,+\,{\frac {n{\sqrt {1-a^{2}x^{2}}}\arcsin(ax)^{n-1}}{a}}\,-\,n\,(n-1)\int \arcsin(ax)^{n-2}\,dx$
$\int \arcsin(ax)^{n}\,dx={\frac {x\arcsin(ax)^{n+2}}{(n+1)\,(n+2)}}\,+\,{\frac {{\sqrt {1-a^{2}x^{2}}}\arcsin(ax)^{n+1}}{a\,(n+1)}}\,-\,{\frac {1}{(n+1)\,(n+2)}}\int \arcsin(ax)^{n+2}\,dx\,,\quad (n\neq -1,-2)$

Arccosine function integration formulas

$\int \arccos(x)\,dx=x\arccos(x)-{\sqrt {1-x^{2}}}+C$
$\int \arccos(ax)\,dx=x\arccos(ax)-{\frac {\sqrt {1-a^{2}x^{2}}}{a}}+C$
$\int x\arccos(ax)\,dx={\frac {x^{2}\arccos(ax)}{2}}-{\frac {\arccos(ax)}{4\,a^{2}}}-{\frac {x{\sqrt {1-a^{2}x^{2}}}}{4\,a}}+C$
$\int x^{2}\arccos(ax)\,dx={\frac {x^{3}\arccos(ax)}{3}}-{\frac {\left(a^{2}x^{2}+2\right){\sqrt {1-a^{2}x^{2}}}}{9\,a^{3}}}+C$
$\int x^{m}\arccos(ax)\,dx={\frac {x^{m+1}\arccos(ax)}{m+1}}\,+\,{\frac {a}{m+1}}\int {\frac {x^{m+1}}{\sqrt {1-a^{2}x^{2}}}}\,dx\,,\quad (m\neq -1)$
$\int \arccos(ax)^{2}\,dx=-2x+x\arccos(ax)^{2}-{\frac {2{\sqrt {1-a^{2}x^{2}}}\arccos(ax)}{a}}+C$
$\int \arccos(ax)^{n}\,dx=x\arccos(ax)^{n}\,-\,{\frac {n{\sqrt {1-a^{2}x^{2}}}\arccos(ax)^{n-1}}{a}}\,-\,n\,(n-1)\int \arccos(ax)^{n-2}\,dx$
$\int \arccos(ax)^{n}\,dx={\frac {x\arccos(ax)^{n+2}}{(n+1)\,(n+2)}}\,-\,{\frac {{\sqrt {1-a^{2}x^{2}}}\arccos(ax)^{n+1}}{a\,(n+1)}}\,-\,{\frac {1}{(n+1)\,(n+2)}}\int \arccos(ax)^{n+2}\,dx\,,\quad (n\neq -1,-2)$

Arctangent function integration formulas

$\int \arctan(x)\,dx=x\arctan(x)-{\frac {\ln \left(x^{2}+1\right)}{2}}+C$
$\int \arctan(ax)\,dx=x\arctan(ax)-{\frac {\ln \left(a^{2}x^{2}+1\right)}{2\,a}}+C$
$\int x\arctan(ax)\,dx={\frac {x^{2}\arctan(ax)}{2}}+{\frac {\arctan(ax)}{2\,a^{2}}}-{\frac {x}{2\,a}}+C$
$\int x^{2}\arctan(ax)\,dx={\frac {x^{3}\arctan(ax)}{3}}+{\frac {\ln \left(a^{2}x^{2}+1\right)}{6\,a^{3}}}-{\frac {x^{2}}{6\,a}}+C$
$\int x^{m}\arctan(ax)\,dx={\frac {x^{m+1}\arctan(ax)}{m+1}}-{\frac {a}{m+1}}\int {\frac {x^{m+1}}{a^{2}x^{2}+1}}\,dx\,,\quad (m\neq -1)$

Arccotangent function integration formulas

$\int \operatorname {arccot}(x)\,dx=x\operatorname {arccot}(x)+{\frac {\ln \left(x^{2}+1\right)}{2}}+C$
$\int \operatorname {arccot}(ax)\,dx=x\operatorname {arccot}(ax)+{\frac {\ln \left(a^{2}x^{2}+1\right)}{2\,a}}+C$
$\int x\operatorname {arccot}(ax)\,dx={\frac {x^{2}\operatorname {arccot}(ax)}{2}}+{\frac {\operatorname {arccot}(ax)}{2\,a^{2}}}+{\frac {x}{2\,a}}+C$
$\int x^{2}\operatorname {arccot}(ax)\,dx={\frac {x^{3}\operatorname {arccot}(ax)}{3}}-{\frac {\ln \left(a^{2}x^{2}+1\right)}{6\,a^{3}}}+{\frac {x^{2}}{6\,a}}+C$
$\int x^{m}\operatorname {arccot}(ax)\,dx={\frac {x^{m+1}\operatorname {arccot}(ax)}{m+1}}+{\frac {a}{m+1}}\int {\frac {x^{m+1}}{a^{2}x^{2}+1}}\,dx\,,\quad (m\neq -1)$

Arcsecant function integration formulas

$\int \operatorname {arcsec}(x)\,dx=x\operatorname {arcsec}(x)\,-\,\ln \left(\left|x\right|+{\sqrt {x^{2}-1}}\right)\,+\,C=x\operatorname {arcsec}(x)-\operatorname {arcosh} |x|+C$
$\int \operatorname {arcsec}(ax)\,dx=x\operatorname {arcsec}(ax)-{\frac {1}{a}}\,\operatorname {arcosh} |ax|+C$
$\int x\operatorname {arcsec}(ax)\,dx={\frac {x^{2}\operatorname {arcsec}(ax)}{2}}-{\frac {x}{2\,a}}{\sqrt {1-{\frac {1}{a^{2}x^{2}}}}}+C$
$\int x^{2}\operatorname {arcsec}(ax)\,dx={\frac {x^{3}\operatorname {arcsec}(ax)}{3}}\,-\,{\frac {\operatorname {arcosh} |ax|}{6\,a^{3}}}\,-\,{\frac {x^{2}}{6\,a}}{\sqrt {1-{\frac {1}{a^{2}x^{2}}}}}\,+\,C$
$\int x^{m}\operatorname {arcsec}(ax)\,dx={\frac {x^{m+1}\operatorname {arcsec}(ax)}{m+1}}\,-\,{\frac {1}{a\,(m+1)}}\int {\frac {x^{m-1}}{\sqrt {1-{\frac {1}{a^{2}x^{2}}}}}}\,dx\,,\quad (m\neq -1)$

Arccosecant function integration formulas

$\int \operatorname {arccsc}(x)\,dx=x\operatorname {arccsc}(x)\,+\,\ln \left(\left|x\right|+{\sqrt {x^{2}-1}}\right)\,+\,C=x\operatorname {arccsc}(x)\,+\,\operatorname {arcosh} |x|\,+\,C$
$\int \operatorname {arccsc}(ax)\,dx=x\operatorname {arccsc}(ax)+{\frac {1}{a}}\,\operatorname {artanh} \,{\sqrt {1-{\frac {1}{a^{2}x^{2}}}}}+C$
$\int x\operatorname {arccsc}(ax)\,dx={\frac {x^{2}\operatorname {arccsc}(ax)}{2}}+{\frac {x}{2\,a}}{\sqrt {1-{\frac {1}{a^{2}x^{2}}}}}+C$
$\int x^{2}\operatorname {arccsc}(ax)\,dx={\frac {x^{3}\operatorname {arccsc}(ax)}{3}}\,+\,{\frac {1}{6\,a^{3}}}\,\operatorname {artanh} \,{\sqrt {1-{\frac {1}{a^{2}x^{2}}}}}\,+\,{\frac {x^{2}}{6\,a}}{\sqrt {1-{\frac {1}{a^{2}x^{2}}}}}\,+\,C$
$\int x^{m}\operatorname {arccsc}(ax)\,dx={\frac {x^{m+1}\operatorname {arccsc}(ax)}{m+1}}\,+\,{\frac {1}{a\,(m+1)}}\int {\frac {x^{m-1}}{\sqrt {1-{\frac {1}{a^{2}x^{2}}}}}}\,dx\,,\quad (m\neq -1)$

See also

Differentiation of trigonometric functions – Mathematical process of finding the derivative of a trigonometric function
List of trigonometric identities – Equalities that involve trigonometric functions
Lists of integrals

References

Lists of integrals
Rational functions Irrational functions Trigonometric functions Inverse trigonometric functions Hyperbolic functions Inverse hyperbolic functions Exponential functions Logarithmic functions Gaussian functions Definite integrals

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.