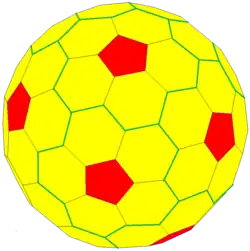
| Order-5 truncated pentagonal hexecontahedron | |
|---|---|
 | |
| Conway | t5gD or wD |
| Goldberg | {5+,3}2,1 |
| Fullerene | C140 |
| Faces | 72: 60 hexagons 12 pentagons |
| Edges | 210 |
| Vertices | 140 |
| Symmetry group | Icosahedral (I) |
| Dual polyhedron | Pentakis snub dodecahedron |
| Properties | convex, chiral |
The order-5 truncated pentagonal hexecontahedron is a convex polyhedron with 72 faces: 60 hexagons and 12 pentagons triangular, with 210 edges, and 140 vertices. Its dual is the pentakis snub dodecahedron.
It is Goldberg polyhedron {5+,3}2,1 in the icosahedral family, with chiral symmetry. The relationship between pentagons steps into 2 hexagons away, and then a turn with one more step.
Construction
It is explicitly called a pentatruncated pentagonal hexecontahedron since only the valence-5 vertices of the pentagonal hexecontahedron are truncated.[2]
Its topology can be constructed in Conway polyhedron notation as t5gD and more simply wD as a whirled dodecahedron, reducing original pentagonal faces and adding 5 distorted hexagons around each, in clockwise or counter-clockwise forms. This picture shows its flat construction before the geometry is adjusted into a more spherical form. The snub can create a (5,3) geodesic polyhedron by k5k6.
Related polyhedra
The whirled dodecahedron creates more polyhedra by basic Conway polyhedron notation. The zip whirled dodecahedron makes a chamfered truncated icosahedron, and Goldberg (4,1). Whirl applied twice produces Goldberg (5,3), and applied twice with reverse orientations produces goldberg (7,0).
| "seed" | ambo | truncate | zip | expand | bevel | snub | chamfer | whirl | whirl-reverse |
|---|---|---|---|---|---|---|---|---|---|
 wD = G(2,1) wD |
 awD awD |
 twD twD |
 zwD = G(4,1) zwD |
 ewD ewD |
 bwD bwD |
 swD swD |
 cwD = G(4,2) cwD |
 wwD = G(5,3) wwD |
 wrwD = G(7,0) wrwD |
| dual | join | needle | kis | ortho | medial | gyro | dual chamfer | dual whirl | dual whirl-reverse |
 dwD dwD |
 jwD jwD |
 nwD nwD |
 kwD kwD |
 owD owD |
 mwD mwD |
 gwD gwD |
 dcwD dcwD |
 dwwD dwwD |
 dwrwD dwrwD |
See also
- Truncated pentagonal icositetrahedron t4gC
References
- ↑ Heinl, Sebastian (2015). "Giant Spherical Cluster with I-C140 Fullerene Topology". Angewandte Chemie International Edition. 54 (45): 13431–13435. doi:10.1002/anie.201505516. PMC 4691335. PMID 26411255.
- ↑ Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination, 2013, Chapter 9 Goldberg polyhedra
- Goldberg, Michael (1937). "A class of multi-symmetric polyhedra". Tohoku Mathematical Journal. 43: 104–108.
- Hart, George (2012). "Goldberg Polyhedra". In Senechal, Marjorie (ed.). Shaping Space (2nd ed.). Springer. pp. 125–138. doi:10.1007/978-0-387-92714-5_9. ISBN 978-0-387-92713-8.
- Hart, George (June 18, 2013). "Mathematical Impressions: Goldberg Polyhedra". Simons Science News.
- Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses, Stan Schein and James Maurice Gaye, PNAS, Early Edition doi: 10.1073/pnas.1310939111
External links
- VRML polyhedral generator Try "t5gI" (Conway polyhedron notation)

