Order-6 octagonal tiling
Order-6 octagonal tiling
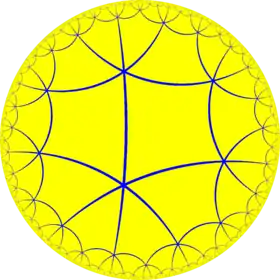
Poincaré disk model of the hyperbolic plane
TypeHyperbolic regular tiling
Vertex configuration86
Schläfli symbol{8,6}
Wythoff symbol6 | 8 2
Coxeter diagram
Symmetry group[8,6], (*862)
DualOrder-8 hexagonal tiling
PropertiesVertex-transitive, edge-transitive, face-transitive

In geometry, the order-6 octagonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {8,6}.

Symmetry

This tiling represents a hyperbolic kaleidoscope of 8 mirrors meeting at a point and bounding regular octagon fundamental domains. This symmetry by orbifold notation is called *33333333 with 8 order-3 mirror intersections. In Coxeter notation can be represented as [8*,6], removing two of three mirrors (passing through the octagon center) in the [8,6] symmetry.

Uniform constructions

There are four uniform constructions of this tiling, three of them as constructed by mirror removal from the [8,6] kaleidoscope. Removing the mirror between the order 2 and 6 points, [8,6,1+], gives [(8,8,3)], (*883). Removing two mirrors as [8,6*], leaves remaining mirrors (*444444).

Four uniform constructions of 8.8.8.8
Uniform
Coloring
Symmetry [8,6]
(*862)
 [8,6,1+] = [(8,8,3)]
(*883)
= 		[8,1+,6]
(*4232)
= 		[8,6*]
(*444444)
Symbol {8,6} {8,6}1⁄2 r(8,6,8)
Coxeter
diagram		 = =

This tiling is topologically related as a part of sequence of regular tilings with octagonal faces, starting with the octagonal tiling, with Schläfli symbol {8,n}, and Coxeter diagram , progressing to infinity.

n82 symmetry mutations of regular tilings: 8n
Space Spherical Compact hyperbolic Paracompact
Tiling
Config. 8.8 83 84 85 86 87 88 ...8∞
Regular tilings {n,6}
Spherical Euclidean Hyperbolic tilings

{2,6}
{3,6}
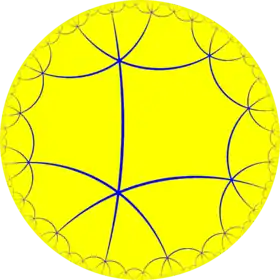
{4,6}
{5,6}
{6,6}
{7,6}
{8,6}
 ...
{∞,6}
Uniform octagonal/hexagonal tilings
Symmetry: [8,6], (*862)
{8,6} t{8,6}
 r{8,6} 2t{8,6}=t{6,8} 2r{8,6}={6,8} rr{8,6} tr{8,6}
Uniform duals
V86 V6.16.16 V(6.8)2 V8.12.12 V68 V4.6.4.8 V4.12.16
Alternations
[1+,8,6]
(*466)		 [8+,6]
(8*3)		 [8,1+,6]
(*4232)		 [8,6+]
(6*4)		 [8,6,1+]
(*883)		 [(8,6,2+)]
(2*43)		 [8,6]+
(862)
h{8,6} s{8,6} hr{8,6} s{6,8} h{6,8} hrr{8,6} sr{8,6}
Alternation duals
V(4.6)6 V3.3.8.3.8.3 V(3.4.4.4)2 V3.4.3.4.3.6 V(3.8)8 V3.45 V3.3.6.3.8

See also

Wikimedia Commons has media related to Order-6 octagonal tiling.

References

  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.