 Full-size (10-ring) *Star board | |
| Designers | Ea Ea |
|---|---|
| Genres | abstract strategy, connection |
| Players | 2 |
*Star is a complex abstract strategy game by Ea Ea, a designer of Y. It is a redevelopment of his earlier game Star.
Notation
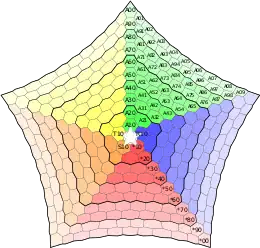
Each cell on the game board is labeled with a three-character value Nxy according to a polar coordinate system:[1]
- N refers to the primary radial arm. There are five arms, labeled as *, S, T, A, or R, proceeding clockwise from the point of the lower right arm of the five-pointed star in the middle of the board
- x refers to the ring number of the cell. The concentric rings are labeled from 1 to 10, using the rightmost digit only, with Ring 1 (x=1) in the center of the board and Ring 10 (x=0) on the perimeter of the board.
- y refers to the tangential position of the cell, counted clockwise from the radial arm. For example, in Ring 3, the cells would be labeled *30 (for the cell on the "*" primary radial arm), *31 (for the cell immediately clockwise within the same ring), *32, S30, S31, S32, T30, ... R31, R32.
This board illustrated here has sectors colored corresponding to the primary radial arms to distinguish the tangential positions (in this example, the "A" sector is colored green). In the game, the board is a single, uniform color.
The perimeter cells (in the ten-ring example illustrated, N0y) are called the pericells and each contain one peri. The five corner pericells (N00 for the ten-ring example) each have one quark associated with them.

The *Star board can also be represented as an equivalent mesh of nodes instead of cells. The same Nxy nomenclature may be used to refer to each node instead.
Rules
*Star can be played on graphs of different sizes. The small, medium, and full boards shown below have 105, 180, and 275 nodes, respectively, of which 30, 40, and 50 are on the perimeter, respectively. Note the five-pointed star in the center acts as a bridge which links the five centermost nodes to each other.
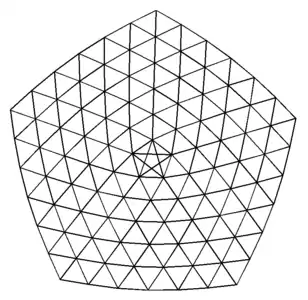 A small *Star board (6 rings, 105 nodes: 30 perimeter and 5 corner nodes)
A small *Star board (6 rings, 105 nodes: 30 perimeter and 5 corner nodes)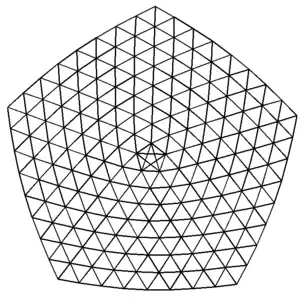 A medium *Star board (8 rings, 180 nodes: 40 perimeter and 5 corner nodes)
A medium *Star board (8 rings, 180 nodes: 40 perimeter and 5 corner nodes)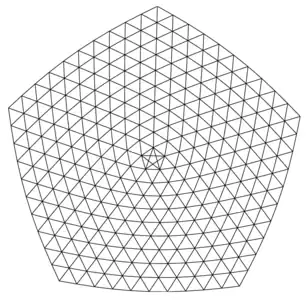 The full *Star board (10 rings, 275 nodes: 50 perimeter and 5 corner nodes)
The full *Star board (10 rings, 275 nodes: 50 perimeter and 5 corner nodes)
Two players alternately place stones of their colour on empty nodes. The game ends when the board is filled up (or when both players agree that the score is decided).
Each node on the perimeter of the board contains one peri. Each corner node contains one quark in addition to the peri for being a perimeter node. A star exists when a connected group of a single color owns at least two peries. A peri is owned if it is either directly occupied by that star, or if the peri is enclosed by the territory occupied by the star.
The game is scored by the sum total of:
- 1 point for each peri owned (occupied or surrounded)
- 1 point to the player with three (or more) quarks (the quark peri)
- An adjustment reward based on the relative number of stars per player
For clarification when computing the score, stars owning fewer than two peries may be removed, making it clear those peries are owned by the surrounding star.
The reward adjustment is computed as the difference between the number of stars the other player has and the number of stars owned by the player, doubled. Effectively, it penalizes the player with more stars and rewards the player who has more effectively grouped their stars. The player with the higher adjusted score wins. In the event of a tie, the player with the most quarks (corners) wins.[1] Under this system, the sum of both players' scores is equal to the number of edge cells (or nodes), plus one. For the "full" board with 10 rings, the total score is 51.[2]: 6
Simplified scoring
As a simplification, each remaining star is worth the number of peries it contains minus four. For example, a group containing exactly two peries is worth 2−4 = −2 points. This is the same as the two peries being given to the opponent. That is, creating a group with just two peries is worthless unless it disconnects opponent groups or contains a corner, which could contribute to the quark peri bonus.
An alternative scoring system has been suggested by R. Wayne Schmittberger. In the alternative system, the score is computed as the number of peries owned by the player, minus the number of peries owned by the opponent, including the quark peri plus an alternative adjustment reward. The alternative adjustment reward is the player's conventional reward adjustment (double the difference in stars) minus the opponent's conventional reward adjustment, which effectively doubles the conventional reward adjustment for both players. Under this system, a player wins if their score is positive.[1]
Scoring example 1
_example_01.svg.png.webp)
In the example game shown here on a 4-ring board, Blue has created a single star, using the five-pointed bridge in the center of the board to connect the two regions. The Blue star owns 7 peries (directly occupying R43, *40, *41, S41, T41, A40, and A41) and 2 quarks (*40 and A40). Red has created three stars with a total of 14 peries (the larger star also connects using the five-pointed bridge and owns 8 peries by occupying 5: *42, S40, A42, R40, and R42 and surrounding 3: *43, A43, and R41; the smaller star owns 3 peries by occupying 2: S42 and T40 and surrounding 1: S43; the smallest star owns 2 peries through occupation of T42 and T43). In addition, Red stars collectively own 3 quarks (S40, T40, and R40), giving Red the quark peri.
Although Red has won more peries (14) than Blue (7), Blue has taken ownership of those 7 peries using 1 star, while Red has created 3 stars. Therefore the Blue reward is 2×(3-1) = +4, while the Red reward is 2×(1-3) = -4. The final score is Blue 7+4=11, Red 14-4=10, and Blue wins this match by more efficiently grouping its pieces.
Using the simplified scoring system, Blue has 7 peries in a single star (-4), for a net total of 3 points. Red has 13 peries in three stars (-12) plus the quark peri (+1), for a total of 2 points.
Under the alternative Schmittberger scoring system, Blue has 7-11+(4-(-4)) = 4 points, while Red has 11-7+(-4-4) = -4 points.
Note that placing additional pieces on the board will not affect the scoring of this game, as the perimeter cells / nodes are all owned by occupation or surrounding pieces, and the stars cannot be further connected.
Scoring example 2
_example_02.svg.png.webp)
In the second example game shown here on a 4-ring board, both Blue and Red have created three stars. The scoring breaks down as:
- Blue
- 10 peries (*43, S41, S42, T40, T43, A40, A42, R40, R41 occupied; S43 surrounded)
- 3 quarks (T40, A40, R40)
- 1 quark peri (owns three quarks)
- Red
- 10 peries (*41, *42, S40, T41, T42, A41, A43, R42, R43 occupied; *40 surrounded)
- 2 quarks (*40, S40)
Because each player has three stars, the reward adjustment is zero for both. The small two-stone star at T43-A40 was key to the win; although it only includes two peries, it crucially includes a third quark, giving Blue a final score of 11 (including the quark peri), edging Red, which scored 10.
Note that although Red has a stone at S43, the peri is not counted as a point for Red, as stars are scored only when there are two or more peries. Instead, the peri is claimed by Blue by surrounding that node.
Development
*Star was derived from Ea Ea's earlier game Star and first published in 2004 by Kadon Enterprises. According to the official rulebook, edited by Irene Schensted from Ea Ea's draft, Mark Thompson, Mariah Williams, and R. Wayne Schmittberger provided constructive input.[2]: 22
Comparison to other games
*Star is closely related to the games Hex and Y where the goal is to connect certain sides of the board to each other. On the other hand, *Star also is closely related to Go in which the goal is to gather more territory than the opponent. Often survival of a group in Go is achieved by connecting it to another one. In Go, all the surrounded area is counted as territory although in practice most of the territory is gathered near the perimeter. Because UCT search was used previously to provide a play-out method for Go, researchers in Finland successfully used a similar algorithm to create a strong computer-based player in 2008.[3]
John McCallion reviewed the game for Games in March 2005, calling it "intriguing" due to "the continuing dilemma that players face" of having to balance scoring by occupying perimeter cells with the need to connect as many scoring groups as possible.[4]
References
- 1 2 3 Ea Ea (September 4, 2001). "*Star". Mindspring. Archived from the original on July 15, 2016.
- 1 2 Ea Ea (2004). "*STAR: Connection game par excellence" (PDF). Kadon Enterprises, Inc. Retrieved 6 June 2022.
- ↑ Raiko, Tapani; Peltonen, Jaakko (2008). Application of UCT Search to the Connection Games of Hex, Y, *Star, and Renkula! (PDF). The Finnish Artificial Intelligence Conference. Espoo. pp. 89–93.
- ↑ McCallion, John J. (March 2005). "*STAR". Games. Retrieved 6 June 2022.
External links
- *Star homepage
- *Star at BoardGameGeek
- Parkes, Sheamus (May 6, 2009). "Re-Worded Rules [for *Star]". BoardGameGeek.