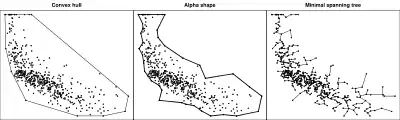
In computational geometry, an alpha shape, or α-shape, is a family of piecewise linear simple curves in the Euclidean plane associated with the shape of a finite set of points. They were first defined by Edelsbrunner, Kirkpatrick & Seidel (1983). The alpha-shape associated with a set of points is a generalization of the concept of the convex hull, i.e. every convex hull is an alpha-shape but not every alpha shape is a convex hull.
Characterization
For each real number α, define the concept of a generalized disk of radius 1/α as follows:
- If α = 0, it is a closed half-plane;
- If α > 0, it is a closed disk of radius 1/α;
- If α < 0, it is the closure of the complement of a disk of radius −1/α.
Then an edge of the alpha-shape is drawn between two members of the finite point set whenever there exists a generalized disk of radius 1/α containing none of the point set and which has the property that the two points lie on its boundary.
If α = 0, then the alpha-shape associated with the finite point set is its ordinary convex hull.
Alpha complex
Alpha shapes are closely related to alpha complexes, subcomplexes of the Delaunay triangulation of the point set.
Each edge or triangle of the Delaunay triangulation may be associated with a characteristic radius, the radius of the smallest empty circle containing the edge or triangle. For each real number α, the α-complex of the given set of points is the simplicial complex formed by the set of edges and triangles whose radii are at most 1/α.
The union of the edges and triangles in the α-complex forms a shape closely resembling the α-shape; however it differs in that it has polygonal edges rather than edges formed from arcs of circles. More specifically, Edelsbrunner (1995) showed that the two shapes are homotopy equivalent. (In this later work, Edelsbrunner used the name "α-shape" to refer to the union of the cells in the α-complex, and instead called the related curvilinear shape an α-body.)
Examples
This technique can be employed to reconstruct a Fermi surface from the electronic Bloch spectral function evaluated at the Fermi level, as obtained from the Green's function in a generalised ab-initio study of the problem. The Fermi surface is then defined as the set of reciprocal space points within the first Brillouin zone, where the signal is highest. The definition has the advantage of covering also cases of various forms of disorder.

See also
References
- N. Akkiraju, H. Edelsbrunner, M. Facello, P. Fu, E. P. Mucke, and C. Varela. "Alpha shapes: definition and software". In Proc. Internat. Comput. Geom. Software Workshop 1995, Minneapolis.
- Edelsbrunner, Herbert (1995), "Smooth surfaces for multi-scale shape representation", Foundations of software technology and theoretical computer science (Bangalore, 1995), Lecture Notes in Comput. Sci., vol. 1026, Berlin: Springer, pp. 391–412, MR 1458090.
- Edelsbrunner, Herbert; Kirkpatrick, David G.; Seidel, Raimund (1983), "On the shape of a set of points in the plane", IEEE Transactions on Information Theory, 29 (4): 551–559, doi:10.1109/TIT.1983.1056714.
External links
- 2D Alpha Shapes and 3D Alpha Shapes in CGAL the Computational Geometry Algorithms Library
- Alpha Complex in the GUDHI library.
- Description and implementation by Duke University
- Everything You Always Wanted to Know About Alpha Shapes But Were Afraid to Ask – with illustrations and interactive demonstration
- Implementation of the 3D alpha-shape for the reconstruction of 3D sets from a point cloud in R
- Description of the implementation details for alpha shapes – lecture providing a description of the formal and intuitive aspects of alpha shape implementation
- Alpha Hulls, Shapes, and Weighted things – lecture slides by Robert Pless at the Washington University in St. Louis