Centered cube number

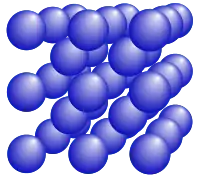
35 points in a body-centered cubic lattice, forming two cubical layers around a central point.
Total no. of terms	Infinity
Subsequence of	Polyhedral numbers
Formula	${\displaystyle n^{3}+(n+1)^{3}}$
First terms	1, 9, 35, 91, 189, 341, 559
OEIS index	A005898 Centered cube

A centered cube number is a centered figurate number that counts the number of points in a three-dimensional pattern formed by a point surrounded by concentric cubical layers of points, with i² points on the square faces of the ith layer. Equivalently, it is the number of points in a body-centered cubic pattern within a cube that has n + 1 points along each of its edges.

The first few centered cube numbers are

1, 9, 35, 91, 189, 341, 559, 855, 1241, 1729, 2331, 3059, 3925, 4941, 6119, 7471, 9009, ... (sequence A005898 in the OEIS).

Formulas

The centered cube number for a pattern with n concentric layers around the central point is given by the formula^[1]

${\displaystyle n^{3}+(n+1)^{3}=(2n+1)\left(n^{2}+n+1\right).}$

The same number can also be expressed as a trapezoidal number (difference of two triangular numbers), or a sum of consecutive numbers, as^[2]

${\displaystyle {\binom {(n+1)^{2}+1}{2}}-{\binom {n^{2}+1}{2}}=(n^{2}+1)+(n^{2}+2)+\cdots +(n+1)^{2}.}$

Properties

Because of the factorization (2n + 1)(n² + n + 1), it is impossible for a centered cube number to be a prime number.^[3] The only centered cube numbers which are also the square numbers are 1 and 9,^[4][5] which can be shown by solving x² = y³ + 3y , the only integer solutions being (x,y) from {(0,0), (1,2), (3,6), (12,42)}, By substituting a=(x-1)/2 and b=y/2, we obtain x^2=2y^3+3y^2+3y+1. This gives only (a,b) from {(-1/2,0), (0,1), (1,3), (11/2,21)} where a,b are half-integers.

See also

• Cube number

References

External links

• Weisstein, Eric W. "Centered Cube Number". MathWorld.