Dissipative solitons (DSs) are stable solitary localized structures that arise in nonlinear spatially extended dissipative systems due to mechanisms of self-organization. They can be considered as an extension of the classical soliton concept in conservative systems. An alternative terminology includes autosolitons, spots and pulses.

Apart from aspects similar to the behavior of classical particles like the formation of bound states, DSs exhibit interesting behavior – e.g. scattering, creation and annihilation – all without the constraints of energy or momentum conservation. The excitation of internal degrees of freedom may result in a dynamically stabilized intrinsic speed, or periodic oscillations of the shape.

Historical development

Experimental observations

Today, DSs can be found in many different experimental set-ups. Examples include

• Gas-discharge systems: plasmas confined in a discharge space which often has a lateral extension large compared to the main discharge length. DSs arise as current filaments between the electrodes and were found in DC systems with a high-ohmic barrier,^[16] AC systems with a dielectric barrier,^[17] and as anode spots,^[18] as well as in an obstructed discharge with metallic electrodes.^[19]

• DSs experimentally observed in planar dc gas-discharge systems with high-ohmic barrier
• 
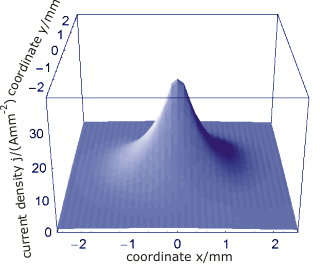  Averaged current density distribution without oscillatory tails.
• 
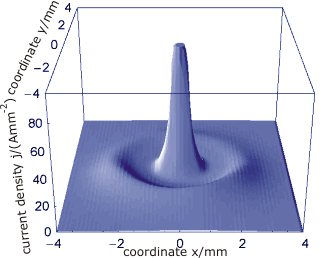  Averaged current density distribution with oscillatory tails.

• Semiconductor systems: these are similar to gas-discharges; however, instead of a gas, semiconductor material is sandwiched between two planar or spherical electrodes. Set-ups include Si and GaAs pin diodes,^[20] n-GaAs,^[21] and Si p⁺−n⁺−p−n⁻,^[22] and ZnS:Mn structures.^[23]
• Nonlinear optical systems: a light beam of high intensity interacts with a nonlinear medium. Typically the medium reacts on rather slow time scales compared to the beam propagation time. Often, the output is fed back into the input system via single-mirror feedback or a feedback loop. DSs may arise as bright spots in a two-dimensional plane orthogonal to the beam propagation direction; one may, however, also exploit other effects like polarization. DSs have been observed for saturable absorbers,^[24] degenerate optical parametric oscillators (DOPOs),^[25] liquid crystal light valves (LCLVs),^[26] alkali vapor systems,^[27] photorefractive media,^[28] and semiconductor microresonators.^[29]
• If the vectorial properties of DSs are considered, vector dissipative soliton could also be observed in a fiber laser passively mode locked through saturable absorber,^[30]
• In addition, multiwavelength dissipative soliton in an all normal dispersion fiber laser passively mode-locked with a SESAM has been obtained. It is confirmed that depending on the cavity birefringence, stable single-, dual- and triple-wavelength dissipative soliton can be formed in the laser. Its generation mechanism can be traced back to the nature of dissipative soliton.^[31]
• Chemical systems: realized either as one- and two-dimensional reactors or via catalytic surfaces, DSs appear as pulses (often as propagating pulses) of increased concentration or temperature. Typical reactions are the Belousov–Zhabotinsky reaction,^[32] the ferrocyanide-iodate-sulphite reaction as well as the oxidation of hydrogen,^[33] CO,^[34] or iron.^[35] Nerve pulses^[11] or migraine aura waves^[36] also belong to this class of systems.
• Vibrated media: vertically shaken granular media,^[37] colloidal suspensions,^[38] and Newtonian fluids^[39] produce harmonically or sub-harmonically oscillating heaps of material, which are usually called oscillons.
• Hydrodynamic systems: the most prominent realization of DSs are domains of convection rolls on a conducting background state in binary liquids.^[40] Another example is a film dragging in a rotating cylindric pipe filled with oil.^[41]
• Electrical networks: large one- or two-dimensional arrays of coupled cells with a nonlinear current–voltage characteristic.^[42] DSs are characterized by a locally increased current through the cells.

Remarkably enough, phenomenologically the dynamics of the DSs in many of the above systems are similar in spite of the microscopic differences. Typical observations are (intrinsic) propagation, scattering, formation of bound states and clusters, drift in gradients, interpenetration, generation, and annihilation, as well as higher instabilities.

Theoretical description

Most systems showing DSs are described by nonlinear partial differential equations. Discrete difference equations and cellular automata are also used. Up to now, modeling from first principles followed by a quantitative comparison of experiment and theory has been performed only rarely and sometimes also poses severe problems because of large discrepancies between microscopic and macroscopic time and space scales. Often simplified prototype models are investigated which reflect the essential physical processes in a larger class of experimental systems. Among these are

• Reaction–diffusion systems, used for chemical systems, gas-discharges and semiconductors.^[43] The evolution of the state vector q(x, t) describing the concentration of the different reactants is determined by diffusion as well as local reactions:

${\displaystyle \partial _{t}{\boldsymbol {q}}={\underline {\boldsymbol {D}}}\,\Delta {\boldsymbol {q}}+{\boldsymbol {R}}({\boldsymbol {q}}).}$

A frequently encountered example is the two-component Fitzhugh–Nagumo-type activator–inhibitor system

${\displaystyle \left({\begin{array}{c}\tau _{u}\,\partial _{t}u\\\tau _{v}\,\partial _{t}v\end{array}}\right)=\left({\begin{array}{cc}d_{u}^{2}&0\\0&d_{v}^{2}\end{array}}\right)\left({\begin{array}{c}\Delta u\\\Delta v\end{array}}\right)+\left({\begin{array}{c}\lambda u-u^{3}-\kappa _{3}v+\kappa _{1}\\u-v\end{array}}\right).}$

Stationary DSs are generated by production of material in the center of the DSs, diffusive transport into the tails and depletion of material in the tails. A propagating pulse arises from production in the leading and depletion in the trailing end.^[44] Among other effects, one finds periodic oscillations of DSs ("breathing"),^[45][46] bound states,^[47] and collisions, merging, generation and annihilation.^[48]

• Ginzburg–Landau type systems for a complex scalar q(x, t) used to describe nonlinear optical systems, plasmas, Bose-Einstein condensation, liquid crystals and granular media.^[49] A frequently found example is the cubic-quintic subcritical Ginzburg–Landau equation

${\displaystyle \partial _{t}q=(d_{r}+id_{i})\,\Delta q+\ell _{r}q+(c_{r}+ic_{i})|q|^{2}q+(q_{r}+iq_{i})|q|^{4}q.}$

To understand the mechanisms leading to the formation of DSs, one may consider the energy ρ = |q|² for which one may derive the continuity equation

${\displaystyle {\begin{aligned}&\partial _{t}\rho +\nabla \cdot {\boldsymbol {m}}=S=d_{r}(q\,\Delta q^{\ast }+q^{\ast }\,\Delta q)+2\ell _{r}\rho +2c_{r}\rho ^{2}+2q_{r}\rho ^{3}\\&{\text{with }}{\boldsymbol {m}}=2d_{i}\operatorname {Im} (q^{\ast }\nabla q).\end{aligned}}}$

One can thereby show that energy is generally produced in the flanks of the DSs and transported to the center and potentially to the tails where it is depleted. Dynamical phenomena include propagating DSs in 1d,^[50] propagating clusters in 2d,^[51] bound states and vortex solitons,^[52] as well as "exploding DSs".^[53]

• The Swift–Hohenberg equation is used in nonlinear optics and in the granular media dynamics of flames or electroconvection. Swift–Hohenberg can be considered as an extension of the Ginzburg–Landau equation. It can be written as

${\displaystyle \partial _{t}q=(s_{r}+is_{i})\,\Delta ^{2}q+(d_{r}+id_{i})\,\Delta q+\ell _{r}q+(c_{r}+ic_{i})|q|^{2}q+(q_{r}+iq_{i})|q|^{4}q.}$

For d_r > 0 one essentially has the same mechanisms as in the Ginzburg–Landau equation.^[54] For d_r < 0, in the real Swift–Hohenberg equation one finds bistability between homogeneous states and Turing patterns. DSs are stationary localized Turing domains on the homogeneous background.^[55] This also holds for the complex Swift–Hohenberg equations; however, propagating DSs as well as interaction phenomena are also possible, and observations include merging and interpenetration.^[56]

• Space-time plots showing the dynamics and interaction of DSs as numerical solutions of the above model equations in one spatial dimension
• 
  Single "breathing" DS as solution of the two-component reaction-diffusion system with activator u (left half) and inhibitor v (right half).
• 
• 

Particle properties and universality

DSs in many different systems show universal particle-like properties. To understand and describe the latter, one may try to derive "particle equations" for slowly varying order parameters like position, velocity or amplitude of the DSs by adiabatically eliminating all fast variables in the field description. This technique is known from linear systems, however mathematical problems arise from the nonlinear models due to a coupling of fast and slow modes.^[57]

Similar to low-dimensional dynamic systems, for supercritical bifurcations of stationary DSs one finds characteristic normal forms essentially depending on the symmetries of the system. E.g., for a transition from a symmetric stationary to an intrinsically propagating DS one finds the Pitchfork normal form

${\displaystyle {\dot {\boldsymbol {v}}}=(\sigma -\sigma _{0}){\boldsymbol {v}}-|{\boldsymbol {v}}|^{2}{\boldsymbol {v}}}$

for the velocity v of the DS,^[58] here σ represents the bifurcation parameter and σ₀ the bifurcation point. For a bifurcation to a "breathing" DS, one finds the Hopf normal form

${\displaystyle {\dot {A}}=(\sigma -\sigma _{0})A-|A|^{2}A}$

for the amplitude A of the oscillation.^[46] It is also possible to treat "weak interaction" as long as the overlap of the DSs is not too large.^[59] In this way, a comparison between experiment and theory is facilitated.^[60][61] Note that the above problems do not arise for classical solitons as inverse scattering theory yields complete analytical solutions.

See also

• Clapotis
• Compacton, a soliton with compact support
• Fiber laser
• Freak waves may be a related phenomenon
• Graphene
• Nonlinear Schrödinger equation
• Nonlinear system
• Oscillon
• Peakon, a soliton with a non-differentiable peak
• Q-ball, a non-topological soliton
• Sine-Gordon equation
• Solitary waves in discrete media^[62]
• Soliton (optics)
• Soliton (topological)
• Soliton model of nerve impulse propagation
• Topological quantum number
• Vector soliton

References