In mathematics, especially in higher-dimensional algebra and homotopy theory, a double groupoid generalises the notion of groupoid and of category to a higher dimension.

Definition

A double groupoid D is a higher-dimensional groupoid involving a relationship for both `horizontal' and `vertical' groupoid structures.^[1] (A double groupoid can also be considered as a generalization of certain higher-dimensional groups.^[2]) The geometry of squares and their compositions leads to a common representation of a double groupoid in the following diagram:

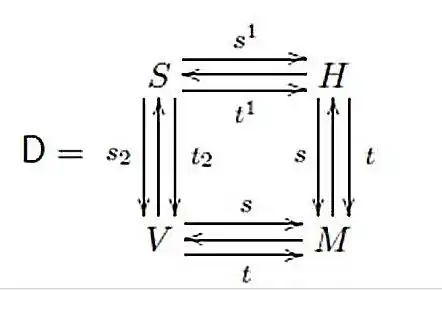
where M is a set of 'points', H and V are, respectively, 'horizontal' and 'vertical' groupoids, and S is a set of 'squares' with two compositions. The composition laws for a double groupoid D make it also describable as a groupoid internal to the category of groupoids.

Given two groupoids H and V over a set M, there is a double groupoid ${\displaystyle \Box (H,V)}$ with H,V as horizontal and vertical edge groupoids, and squares given by quadruples

${\displaystyle {\begin{pmatrix}&h&\\[-0.9ex]v&&v'\\[-0.9ex]&h'&\end{pmatrix}}}$

for which one assumes always that h, h′ are in H and v, v′ are in V, and that the initial and final points of these edges match in M as suggested by the notation; that is for example sh = sv, th = sv', ..., etc. The compositions are to be inherited from those of H,V; that is:

${\displaystyle {\begin{pmatrix}&h&\\[-0.9ex]v&&v'\\[-0.9ex]&h'&\end{pmatrix}}\circ _{1}{\begin{pmatrix}&h'&\\[-0.9ex]w&&w'\\[-0.9ex]&h''&\end{pmatrix}}={\begin{pmatrix}&h&\\[-0.9ex]vw&&v'w'\\[-0.9ex]&h''&\end{pmatrix}}}$

and

${\displaystyle {\begin{pmatrix}&h&\\[-0.9ex]v&&v'\\[-0.9ex]&h'&\end{pmatrix}}\circ _{2}{\begin{pmatrix}&k&\\[-0.9ex]v'&&v''\\[-0.9ex]&k'&\end{pmatrix}}={\begin{pmatrix}&hk&\\[-0.9ex]v&&v''\\[-0.9ex]&h'k'&\end{pmatrix}}}$

This construction is the right adjoint to the forgetful functor which takes the double groupoid as above, to the pair of groupoids H,V over M.

Other related constructions are that of a double groupoid with connection^[3] and homotopy double groupoids.^[4] The homotopy double groupoid of a pair of pointed spaces is a key element of the proof of a two-dimensional Seifert-van Kampen Theorem, first proved by Brown and Higgins in 1978,^[5] and given an extensive treatment in the book.^[6]

Examples

An easy class of examples can be cooked up by considering crossed modules, or equivalently the data of a morphism of groups

${\displaystyle [G_{1}\xrightarrow {\phi } G_{0}]}$

which has an equivalent description as the groupoid internal to the category of groups

${\displaystyle s,t:G_{0}\times G_{1}\to G_{0}}$

where

${\displaystyle {\begin{matrix}s(g_{0},g_{1})=g_{0}&t(g_{0},g_{1})=\phi (g_{1})g_{0}\end{matrix}}}$

are the structure morphisms for this groupoid. Since groups embed in the category of groupoids sending a group ${\displaystyle G}$ to the category ${\displaystyle {\textbf {B}}G}$ with a single object and morphisms giving the group ${\displaystyle G}$, the structure above gives a double groupoid. Let's give an explicit example: from the group extension

${\displaystyle 1\to \mathbb {Z} _{4}\to Q_{8}\to \mathbb {Z} _{2}\to 1}$

and the embedding of ${\displaystyle \mathbb {Z} _{2}\to \mathbb {Z} _{4}}$, there is an associated double groupoid from the two term complex of groups

${\displaystyle Q_{8}\to \mathbb {Z} _{4}}$

with kernel is ${\displaystyle \mathbb {Z} _{4}}$ and cokernel is given by ${\displaystyle \mathbb {Z} _{2}}$. This gives an associated homotopy type ${\displaystyle X}$^[7] with

${\displaystyle \pi _{1}(X)=\mathbb {Z} _{2}}$ and ${\displaystyle \pi _{2}(X)=\mathbb {Z} _{4}}$

Its postnikov invariant can be determined by the class of ${\displaystyle Q_{8}\to \mathbb {Z} _{4}}$ in the group cohomology group ${\displaystyle H^{3}(\mathbb {Z} _{2},\mathbb {Z} _{4})\cong \mathbb {Z} /2}$. Because this is not a trivial crossed-module, it's postnikov invariant is ${\displaystyle 1}$, giving a homotopy type which is not equivalent to the geometric realization of a simplicial abelian group.

Homotopy double groupoid

A generalisation to dimension 2 of the fundamental groupoid on a set of base was given by Brown and Higgins in 1978 as follows. Let ${\displaystyle (X,A,C)}$ be a triple of spaces, i.e. ${\displaystyle C\subseteq A\subseteq X}$. Define ${\displaystyle \rho (X,A,C)}$ to be the set of homotopy classes rel vertices of maps of a square into X which take the edges into A and the vertices into C. It is not entirely trivial to prove that the natural compositions of such squares in two directions are inherited by these homotopy classes to give a double groupoid, which also has an extra structure of so-called connections necessary to discuss the idea of commutative cube in a double groupoid. This double groupoid is used in an essential way to prove a two-dimensional Seifert-van Kampen theorem, which gives new information and computations on second relative homotopy groups as part of a crossed module. For more information, see Part I of the book by Brown, Higgins, Sivera listed below.

Convolution algebra

A convolution C*-algebra of a double groupoid can also be constructed by employing the square diagram D of a double groupoid.^[8]

Double groupoid category

The category whose objects are double groupoids and whose morphisms are double groupoid homomorphisms that are double groupoid diagram (D) functors is called the double groupoid category, or the category of double groupoids.

See also

• 2-group
• Crossed module
• N-group (category theory)
• ∞-groupoid

Notes

This article incorporates material from higher dimensional algebra on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

References

• Brown, Ronald and C.B. Spencer: "Double groupoids and crossed modules", Cahiers Top. Geom. Diff.. 17 (1976), 343–362.
• Brown, R., Hardie, K., Kamps, H. and T. Porter: 2002, "The homotopy double groupoid of a Hausdorff space.", Theory and Applications of Categories: 10,71–93
• Brown, Ronald, 1987, "From groups to groupoids: a brief survey," Bull. London Math. Soc. 19: 113–34. Reviews the history of groupoids up to 1987, starting with the work of Brandt on quadratic forms. The downloadable version updates the many references.
• Brown, Ronald,, 2006. Topology and groupoids. Booksurge. Revised and extended edition of a book previously published in 1968 and 1988. Groupoids are introduced in the context of their topological application.
• Brown, Ronald,, Higher-dimensional group theory. Explains how the groupoid concept has led to higher-dimensional homotopy groupoids, having applications in homotopy theory and in group cohomology.
• F. Borceux, G. Janelidze, 2001, Galois theories. Cambridge Univ. Press. Shows how generalisations of Galois theory lead to Galois groupoids.
• Cannas da Silva, A., and A. Weinstein, Geometric Models for Noncommutative Algebras. Especially Part VI.
• Golubitsky, M., Ian Stewart, 2006, "Nonlinear dynamics of networks: the groupoid formalism", Bull. Amer. Math. Soc. 43: 305–64
• Higgins, P. J., "The fundamental groupoid of a graph of groups", J. London Math. Soc. (2) 13 (1976) 145–149.
• Higgins, P. J. and Taylor, J., "The fundamental groupoid and the homotopy crossed complex of an orbit space", in Category theory (Gummersbach, 1981), Lecture Notes in Math., Volume 962. Springer, Berlin (1982), 115–122.
• Higgins, P. J., 1971. Categories and groupoids. Van Nostrand Notes in Mathematics. Republished in Reprints in Theory and Applications of Categories, No. 7 (2005) pp. 1–195; freely downloadable. Substantial introduction to category theory with special emphasis on groupoids. Presents applications of groupoids in group theory, for example to a generalisation of Grushko's theorem, and in topology, e.g. fundamental groupoid.
• http://planetphysics.org/encyclopedia/DoubleGroupoidWithConnection.html%5B%5D "Double Groupoid with Connection".
• Weinstein, Alan, "Groupoids: unifying internal and external symmetry – A tour though some examples." Also available in Postscript., Notices of the AMS, July 1996, pp. 744–752.