Fixed-point computation

Fixed-point computation refers to the process of computing an exact or approximate fixed point of a given function.^[1] In its most common form, we are given a function f that satisfies the condition to the Brouwer fixed-point theorem, that is: f is continuous and maps the unit d-cube to itself. The Brouwer fixed-point theorem guarantees that f has a fixed point, but the proof is not constructive. Various algorithms have been devised for computing an approximate fixed point. Such algorithms are used in economics for computing a market equilibrium, in game theory for computing a Nash equilibrium, and in dynamic system analysis.

Definitions

The graph of an example function with three fixed points

The unit interval is denoted by $E:=[0,1]$ , and the unit d-dimensional cube is denoted by E^d. A continuous function f is defined on E^d (from E^d to itself). Often, it is assumed that f is not only continuous but also Lipschitz continuous, that is, for some constant L, $|f(x)-f(y)|\leq L\cdot |x-y|$ for all x,y in E^d.

A fixed point of f is a point x in E^d such that f(x) = x. By the Brouwer fixed-point theorem, any continuous function from E^d to itself has a fixed point. But for general functions, it is impossible to compute a fixed point precisely, since it can be an arbitrary real number. Fixed-point computation algorithms look for approximate fixed points. There are several criteria for an approximate fixed point. Several common criteria are:^[2]

The residual criterion: given an approximation parameter $\varepsilon >0$ , An $ε$ -residual fixed-point of f is a point x in E^d such that $|f(x)-x|\leq \varepsilon$ , where here |.| denotes the maximum norm. That is, all d coordinates of the difference $f(x)-x$ should be at most $ε$ .^[3]^: 4
The absolute criterion: given an approximation parameter $\delta >0$ , A δ-absolute fixed-point of f is a point x in E^d such that $|x-x_{0}|\leq \delta$ , where $x_{0}$ is any fixed-point of f.
The relative criterion: given an approximation parameter $\delta >0$ , A δ-relative fixed-point of f is a point x in E^d such that $|x-x_{0}|/|x_{0}|\leq \delta$ , where $x_{0}$ is any fixed-point of f.

For Lipschitz-continuous functions, the absolute criterion is stronger than the residual criterion: If f is Lipschitz-continuous with constant L, then $|x-x_{0}|\leq \delta$ implies $|f(x)-f(x_{0})|\leq L\cdot \delta$ . Since $x_{0}$ is a fixed-point of f, this implies $|f(x)-x_{0}|\leq L\cdot \delta$ , so $|f(x)-x|\leq (1+L)\cdot \delta$ . Therefore, a δ-absolute fixed-point is also an $ε$ -residual fixed-point with $\varepsilon =(1+L)\cdot \delta$ .

The most basic step of a fixed-point computation algorithm is a value query: given any x in E^d, the

The function f is accessible via evaluation queries: for any x, the algorithm can evaluate f(x). The run-time complexity of an algorithm is usually given by the number of required evaluations.

Contractive functions

A Lipschitz-continuous function with constant L is called contractive if L < 1; it is called weakly-contractive if L ≤ 1.Every contractive function satisfying Brouwer's condisions has a unique fixed point. Moreover, fixed-point computation for contractive functions is easier than for general functions.

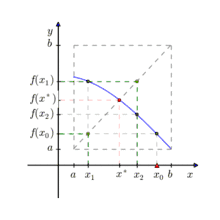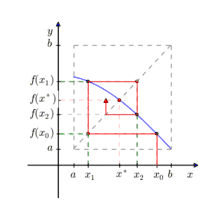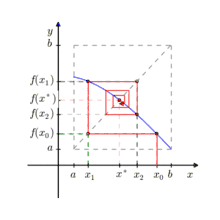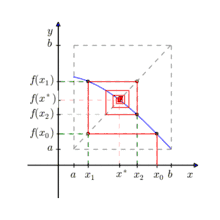
Computing a fixed point using function iteration

The first algorithm for fixed-point computation was the fixed-point iteration algorithm of Banach. Banach's fixed-point theorem implies that, when fixed-point iteration is applied to a contraction mapping, the error after t iterations is in $O(L^{t})$ . Therefore, the number of evaluations required for a δ-relative fixed-point is approximately $\log _{L}(\delta )=\log(\delta )/\log(L)=\log(1/\delta )/\log(1/L)$ . Sikorski and Wozniakowski^[4] showed that Banach's algorithm is optimal when the dimension is large. Specifically, when $d\geq \log(1/\delta )/\log(1/L)$ , the number of required evaluations of any algorithm for δ-relative fixed-point is larger than 50% the number of evaluations required by the iteration algorithm. Note that when L approaches 1, the number of evaluations approaches infinity. In fact, no finite algorithm can compute a δ-absolute fixed point for all functions with L=1.^[5]

When L < 1 and d = 1, the optimal algorithm is the Fixed Point Envelope (FPE) algorithm of Sikorski and Wozniakowski.^[4] It finds a δ-relative fixed point using $O(\log(1/\delta )+\log \log(1/(1-L)))$ queries, and a δ-absolute fixed point using $O(\log(1/\delta ))$ queries. This is much faster than the fixed-point iteration algorithm.^[6]

When d>1 but not too large, and L ≤ 1, the optimal algorithm is the interior-ellipsoid algorithm (based on the ellipsoid method).^[7] It finds an $ε$ -residual fixed-point is using $O(d\cdot \log(1/\varepsilon ))$ evaluations. When L<1, it finds a δ-absolute fixed point using $O(d\cdot [\log(1/\delta )+\log(1/(1-L))])$ evaluations.

Shellman and Sikorski^[8] presented an algorithm called BEFix (Bisection Envelope Fixed-point) for computing an $ε$ -residual fixed-point of a two-dimensional function with L ≤ 1, using only $2\lceil \log _{2}(1/\varepsilon )\rceil +1$ queries. They later^[9] presented an improvement called BEDFix (Bisection Envelope Deep-cut Fixed-point), with the same worst-case guarantee but better empirical performance. When L<1, BEDFix can also compute a δ-absolute fixed-point using $O(\log(1/\varepsilon )+\log(1/(1-L)))$ queries.

Shellman and Sikorski^[2] presented an algorithm called PFix for computing an $ε$ -residual fixed-point of a d-dimensional function with L ≤ 1, using $O(\log ^{d}(1/\varepsilon ))$ queries. When L < 1, PFix can be executed with $\varepsilon =(1-L)\cdot \delta$ , and in that case, it computes a δ-absolute fixed-point, using $O(\log ^{d}(1/[(1-L)\delta ]))$ queries. It is more efficient than the iteration algorithm when L is close to 1. The algorithm is recursive: it handles a d-dimensional function by recursive calls on (d-1)-dimensional functions.

Algorithms for differentiable functions

When the function f is differentiable, and the algorithm can evaluate its derivative (not only f itself), the Newton method can be used and it is much faster.^[10]^[11]

General functions

For functions with Lipschitz constant L > 1, computing a fixed-point is much harder.

One dimension

For a 1-dimensional function (d = 1), a δ-absolute fixed-point can be found using $O(\log(1/\delta ))$ queries using the bisection method: start with the interval $E:=[0,1]$ ; at each iteration, let x be the center of the current interval, and compute f(x); if f(x) > x then recurse on the sub-interval to the right of x; otherwise, recurse on the interval to the left of x. Note that the current interval always contains a fixed point, so after $O(\log(1/\delta ))$ queries, any point in the remaining interval is a δ-absolute fixed-point of f. Setting ${\displaystyle \delta$ , where L is the Lipschitz constant, gives an $ε$ -residual fixed-point, using $O(\log(L/\varepsilon )=\log(L)+\log(1/\varepsilon ))$ queries.^[3]

Two or more dimensions

For functions in two or more dimensions, the problem is much more challenging. Shellman and Sikorski^[2] proved that, for any integers d ≥ 2 and L > 1, finding a δ-absolute fixed-point of d-dimensional L-Lipschitz functions might require infinitely-many evaluations. The proof idea is as follows. For any integer T > 1, and for any sequence of T of evaluation queries (possibly adaptive), one can construct two functions that are Lipschitz-continuous with constant L, and yield the same answer to all these queries, but one of them has a unique fixed-point at (x, 0) and the other has a unique fixed-point at (x, 1). Any algorithm using T evaluations cannot differentiate between these functions, so cannot find a δ-absolute fixed-point. This is true for any finite integer T.

Several algorithms based on function evaluations have been developed for finding an $ε$ -residual fixed-point

The first algorithm to approximate a fixed point of a general function was developed by Herbert Scarf in 1967.^[12]^[13] Scarf's algorithm finds an $ε$ -residual fixed-point by finding a fully-labelled "primitive set", in a construction similar to Sperner's lemma.
A later algorithm by Harold Kuhn^[14] used simplices and simplicial partitions instead of primitive sets.
Developing the simplicial approach further, Orin Harrison Merrill^[15] presented the restart algorithm.
B. Curtis Eaves^[16] presented the homotopy algorithm. The algorithm works by starting with an affine function that approximates f, and deforming it towards f, while following the fixed point. A book by Michael Todd^[1] surveys various algorithms developed until 1976.
David Gale^[17] showed that computing a fixed point of an n-dimensional function (on the unit d-dimensional cube) is equivalent to deciding who is the winner in a d-dimensional game of Hex (a game with d players, each of whom needs to connect two opposite faces of a d-cube). Given the desired accuracy $ε$
- Construct a Hex board of size kd, where $k>1/\varepsilon$ . Each vertex z corresponds to a point z/k in the unit n-cube.
- Compute the difference f(z/k) - z/k; note that the difference is an n-vector.
- Label the vertex z by a label in 1, ..., d, denoting the largest coordinate in the difference vector.
- The resulting labeling corresponds to a possible play of the d-dimensional Hex game among d players. This game must have a winner, and Gale presents an algorithm for constructing the winning path.
- In the winning path, there must be a point in which f_i(z/k) - z/k is positive, and an adjacent point in which f_i(z/k) - z/k is negative. This means that there is a fixed point of f between these two points.

In the worst case, the number of function evaluations required by all these algorithms is exponential in the binary representation of the accuracy, that is, in $\Omega (1/\varepsilon )$ .

Query complexity

Hirsch, Papadimitriou and Vavasis proved that^[3] any algorithm based on function evaluations, that finds an $ε$ -residual fixed-point of f, requires $\Omega (L'/\varepsilon )$ function evaluations, where $L'$ is the Lipschitz constant of the function $f(x)-x$ (note that $L-1\leq L'\leq L+1$ ). More precisely:

For a 2-dimensional function (d=2), they prove a tight bound $\Theta (L'/\varepsilon )$ .
For any d ≥ 3, finding an $ε$ -residual fixed-point of a d-dimensional function requires $\Omega ((L'/\varepsilon )^{d-2})$ queries and $O((L'/\varepsilon )^{d})$ queries.

The latter result leaves a gap in the exponent. Chen and Deng^[18] closed the gap. They proved that, for any d ≥ 2 and $1/\varepsilon >4d$ and $L'/\varepsilon >192d^{3}$ , the number of queries required for computing an $ε$ -residual fixed-point is in $\Theta ((L'/\varepsilon )^{d-1})$ .

Discrete fixed-point computation

A discrete function is a function defined on a subset of $\mathbb {Z} ^{d}$ (the d-dimensional integer grid). There are several discrete fixed-point theorems, stating conditions under which a discrete function has a fixed point. For example, the Iimura-Murota-Tamura theorem states that (in particular) if f is a function from a rectangle subset of $\mathbb {Z} ^{d}$ to itself, and f is hypercubic direction-preserving, then f has a fixed point.

Let f be a direction-preserving function from the integer cube $\{1,\dots ,n\}^{d}$ to itself. Chen and Deng^[18] prove that, for any d ≥ 2 and n > 48d, computing such a fixed point requires $\Theta (n^{d-1})$ function evaluations.

Chen and Deng^[19] define a different discrete-fixed-point problem, which they call 2D-BROUWER. It considers a discrete function f on $\{0,\dots ,n\}^{2}$ such that, for every x on the grid, f(x) - x is either (0, 1) or (1, 0) or (-1, -1). The goal is to find a square in the grid, in which all three labels occur. The function f must map the square $\{0,\dots ,n\}^{2}$ to itself, so it must map the lines x = 0 and y = 0 to either (0, 1) or (1, 0); the line x = n to either (-1, -1) or (0, 1); and the line y = n to either (-1, -1) or (1,0). The problem can be reduced to 2D-SPERNER (computing a fully-labeled triangle in a triangulation satisfying the conditions to Sperner's lemma), and therefore it is PPAD-complete. This implies that computing an approximate fixed-point is PPAD-complete even for very simple functions.

Relation between fixed-point computation and root-finding algorithms

Given a function g from E^d to R, a root of g is a point x in E^d such that g(x)=0. An $ε$ -root of g is a point x in E^d such that $g(x)\leq \varepsilon$ .

Fixed-point computation is a special case of root-finding: given a function f on E^d, define $g(x):=|f(x)-x|$ . Clearly, x is a fixed-point of f if and only if x is a root of g, and x is an $ε$ -residual fixed-point of f if and only if x is an $ε$ -root of g. Therefore, any root-finding algorithm (an algorithm that computes an approximate root of a function) can be used to find an approximate fixed-point.

The opposite is not true: finding an approximate root of a general function may be harder than finding an approximate fixed point. In particular, Sikorski^[20] proved that finding an $ε$ -root requires $\Omega (1/\varepsilon ^{d})$ function evaluations. This gives an exponential lower bound even for a one-dimensional function (in contrast, an $ε$ -residual fixed-point of a one-dimensional function can be found using $O(\log(1/\varepsilon ))$ queries using the bisection method). Here is a proof sketch.^[3]^: 35 Construct a function g that is slightly larger than $ε$ everywhere in E^d except in some small cube around some point x₀, where x₀ is the unique root of g. If g is Lipschitz continuous with constant L, then the cube around x₀ can have a side-length of $\varepsilon /L$ . Any algorithm that finds an $ε$ -root of g must check a set of cubes that covers the entire E^d; the number of such cubes is at least $(L/\varepsilon )^{d}$ .

However, there are classes of functions for which finding an approximate root is equivalent to finding an approximate fixed point. One example^[18] is the class of functions g such that $g(x)+x$ maps E^d to itself (that is: $g(x)+x$ is in E^d for all x in E^d). This is because, for every such function, the function $f(x):=g(x)+x$ satisfies the conditions to Brouwer's fixed-point theorem. Clearly, x is a fixed-point of f if and only if x is a root of g, and x is an $ε$ -residual fixed-point of f if and only if x is an $ε$ -root of g. Chen and Deng^[18] show that the discrete variants of these problems are computationally equivalent: both problems require $\Theta (n^{d-1})$ function evaluations.

Communication complexity

Roughgarden and Weinstein^[21] studied the communication complexity of computing an approximate fixed-point. In their model, there are two agents: one of them knows a function f and the other knows a function g. Both functions are Lipschitz continuous and satisfy Brouwer's conditions. The goal is to compute an approximate fixed point of the composite function $g\circ f$ . They show that the deterministic communication complexity is in $\Omega (2^{d})$ .

References

1 2 The Computation of Fixed Points and Applications. Lecture Notes in Economics and Mathematical Systems. Vol. 124. 1976. doi:10.1007/978-3-642-50327-6. ISBN 978-3-540-07685-8.
1 2 3 Shellman, Spencer; Sikorski, K. (December 2003). "A recursive algorithm for the infinity-norm fixed point problem". Journal of Complexity. 19 (6): 799–834. doi:10.1016/j.jco.2003.06.001.
1 2 3 4 Hirsch, Michael D; Papadimitriou, Christos H; Vavasis, Stephen A (December 1989). "Exponential lower bounds for finding Brouwer fix points". Journal of Complexity. 5 (4): 379–416. doi:10.1016/0885-064X(89)90017-4. S2CID 1727254.
1 2 Sikorski, K; Woźniakowski, H (December 1987). "Complexity of fixed points, I". Journal of Complexity. 3 (4): 388–405. doi:10.1016/0885-064X(87)90008-2.
↑ Sikorski, Krzysztof A. (2001). Optimal Solution of Nonlinear Equations. Oxford University Press. ISBN 978-0-19-510690-9.
↑ Sikorski, K. (1989). "Fast Algorithms for the Computation of Fixed Points". Robustness in Identification and Control. pp. 49–58. doi:10.1007/978-1-4615-9552-6_4. ISBN 978-1-4615-9554-0.
↑ Huang, Z; Khachiyan, L; Sikorski, K (June 1999). "Approximating Fixed Points of Weakly Contracting Mappings". Journal of Complexity. 15 (2): 200–213. doi:10.1006/jcom.1999.0504.
↑ Shellman, Spencer; Sikorski, K. (June 2002). "A Two-Dimensional Bisection Envelope Algorithm for Fixed Points". Journal of Complexity. 18 (2): 641–659. doi:10.1006/jcom.2001.0625.
↑ Shellman, Spencer; Sikorski, K. (September 2003). "Algorithm 825: A deep-cut bisection envelope algorithm for fixed points". ACM Transactions on Mathematical Software. 29 (3): 309–325. doi:10.1145/838250.838255. S2CID 7786886.
↑ Kellogg, R. B.; Li, T. Y.; Yorke, J. (September 1976). "A Constructive Proof of the Brouwer Fixed-Point Theorem and Computational Results". SIAM Journal on Numerical Analysis. 13 (4): 473–483. doi:10.1137/0713041.
↑ Smale, Steve (July 1976). "A convergent process of price adjustment and global newton methods". Journal of Mathematical Economics. 3 (2): 107–120. doi:10.1016/0304-4068(76)90019-7.
↑ Scarf, Herbert (September 1967). "The Approximation of Fixed Points of a Continuous Mapping". SIAM Journal on Applied Mathematics. 15 (5): 1328–1343. doi:10.1137/0115116.
↑ H. Scarf found the first algorithmic proof: Voitsekhovskii, M.I. (2001) [1994], "Brouwer theorem", Encyclopedia of Mathematics, EMS Press, ISBN 1-4020-0609-8.
↑ Kuhn, Harold W. (1968). "Simplicial Approximation of Fixed Points". Proceedings of the National Academy of Sciences of the United States of America. 61 (4): 1238–1242. doi:10.1073/pnas.61.4.1238. JSTOR 58762. PMC 225246. PMID 16591723.
↑ Merrill, Orin Harrison (1972). Applications and Extensions of an Algorithm that Computes Fixed Points of Certain Upper Semi-continuous Point to Set Mappings (Thesis). OCLC 570461463. NAID 10006142329.
↑ Eaves, B. Curtis (December 1972). "Homotopies for computation of fixed points". Mathematical Programming. 3–3 (1): 1–22. doi:10.1007/BF01584975. S2CID 39504380.
↑ Gale, David (1979). "The Game of Hex and Brouwer Fixed-Point Theorem". The American Mathematical Monthly. 86 (10): 818–827. doi:10.2307/2320146. JSTOR 2320146.
1 2 3 4 Chen, Xi; Deng, Xiaotie (2005). "On algorithms for discrete and approximate brouwer fixed points". Proceedings of the thirty-seventh annual ACM symposium on Theory of computing. pp. 323–330. doi:10.1145/1060590.1060638. ISBN 1581139608. S2CID 16942881.
↑ Chen, Xi; Deng, Xiaotie (October 2009). "On the complexity of 2D discrete fixed point problem". Theoretical Computer Science. 410 (44): 4448–4456. doi:10.1016/j.tcs.2009.07.052. S2CID 2831759.
↑ Sikorski, K. (June 1984). "Optimal solution of nonlinear equations satisfying a Lipschitz condition". Numerische Mathematik. 43 (2): 225–240. doi:10.1007/BF01390124. S2CID 120937024.
↑ Roughgarden, Tim; Weinstein, Omri (2016). "On the Communication Complexity of Approximate Fixed Points". 2016 IEEE 57th Annual Symposium on Foundations of Computer Science (FOCS). pp. 229–238. doi:10.1109/FOCS.2016.32. ISBN 978-1-5090-3933-3. S2CID 87553.