In mathematics, a graph C*-algebra is a universal C*-algebra constructed from a directed graph. Graph C*-algebras are direct generalizations of the Cuntz algebras and Cuntz-Krieger algebras, but the class of graph C*-algebras has been shown to also include several other widely studied classes of C*-algebras. As a result, graph C*-algebras provide a common framework for investigating many well-known classes of C*-algebras that were previously studied independently. Among other benefits, this provides a context in which one can formulate theorems that apply simultaneously to all of these subclasses and contain specific results for each subclass as special cases.

Although graph C*-algebras include numerous examples, they provide a class of C*-algebras that are surprisingly amenable to study and much more manageable than general C*-algebras. The graph not only determines the associated C*-algebra by specifying relations for generators, it also provides a useful tool for describing and visualizing properties of the C*-algebra. This visual quality has led to graph C*-algebras being referred to as "operator algebras we can see."^[1][2] Another advantage of graph C*-algebras is that much of their structure and many of their invariants can be readily computed. Using data coming from the graph, one can determine whether the associated C*-algebra has particular properties, describe the lattice of ideals, and compute K-theoretic invariants.

Graph terminology

The terminology for graphs used by C*-algebraists differs slightly from that used by graph theorists. The term graph is typically taken to mean a directed graph ${\displaystyle E=(E^{0},E^{1},r,s)}$ consisting of a countable set of vertices ${\displaystyle E^{0}}$, a countable set of edges ${\displaystyle E^{1}}$, and maps ${\displaystyle r,s:E^{1}\rightarrow E^{0}}$ identifying the range and source of each edge, respectively. A vertex ${\displaystyle v\in E^{0}}$ is called a sink when ${\displaystyle s^{-1}(v)=\emptyset }$; i.e., there are no edges in ${\displaystyle E}$ with source ${\displaystyle v}$. A vertex ${\displaystyle v\in E^{0}}$ is called an infinite emitter when ${\displaystyle s^{-1}(v)}$ is infinite; i.e., there are infinitely many edges in ${\displaystyle E}$ with source ${\displaystyle v}$. A vertex is called a singular vertex if it is either a sink or an infinite emitter, and a vertex is called a regular vertex if it is not a singular vertex. Note that a vertex ${\displaystyle v}$ is regular if and only if the number of edges in ${\displaystyle E}$ with source ${\displaystyle v}$ is finite and nonzero. A graph is called row-finite if it has no infinite emitters; i.e., if every vertex is either a regular vertex or a sink.

A path is a finite sequence of edges ${\displaystyle e_{1}e_{2}\ldots e_{n}}$ with ${\displaystyle r(e_{i})=s(e_{i+1})}$ for all ${\displaystyle 1\leq i\leq n-1}$. An infinite path is a countably infinite sequence of edges ${\displaystyle e_{1}e_{2}\ldots }$ with ${\displaystyle r(e_{i})=s(e_{i+1})}$ for all ${\displaystyle i\geq 1}$. A cycle is a path ${\displaystyle e_{1}e_{2}\ldots e_{n}}$ with ${\displaystyle r(e_{n})=s(e_{1})}$, and an exit for a cycle ${\displaystyle e_{1}e_{2}\ldots e_{n}}$ is an edge ${\displaystyle f\in E^{1}}$ such that ${\displaystyle s(f)=s(e_{i})}$ and ${\displaystyle f\neq e_{i}}$ for some ${\displaystyle 1\leq i\leq n}$. A cycle ${\displaystyle e_{1}e_{2}\ldots e_{n}}$ is called a simple cycle if ${\displaystyle s(e_{i})\neq s(e_{1})}$ for all ${\displaystyle 2\leq i\leq n}$.

The following are two important graph conditions that arise in the study of graph C*-algebras.

Condition (L): Every cycle in the graph has an exit.

Condition (K): There is no vertex in the graph that is on exactly one simple cycle. That is, a graph satisfies Condition (K) if and only if each vertex in the graph is either on no cycles or on two or more simple cycles.

The Cuntz-Krieger Relations and the universal property

A Cuntz-Krieger ${\displaystyle E}$-family is a collection ${\displaystyle \left\{s_{e},p_{v}:e\in E^{1},v\in E^{0}\right\}}$ in a C*-algebra such that the elements of ${\displaystyle \left\{s_{e}:e\in E^{1}\right\}}$ are partial isometries with mutually orthogonal ranges, the elements of ${\displaystyle \left\{p_{v}:v\in E^{0}\right\}}$ are mutually orthogonal projections, and the following three relations (called the Cuntz-Krieger relations) are satisfied:

1. (CK1) ${\displaystyle s_{e}^{*}s_{e}=p_{r(e)}}$ for all ${\displaystyle e\in E^{1}}$,
2. (CK2) ${\displaystyle p_{v}=\sum _{s(e)=v}s_{e}s_{e}^{*}}$ whenever ${\displaystyle v}$ is a regular vertex, and
3. (CK3) ${\displaystyle s_{e}s_{e}^{*}\leq p_{s(e)}}$ for all ${\displaystyle e\in E^{1}}$.

The graph C*-algebra corresponding to ${\displaystyle E}$, denoted by ${\displaystyle C^{*}(E)}$, is defined to be the C*-algebra generated by a Cuntz-Krieger ${\displaystyle E}$-family that is universal in the sense that whenever ${\displaystyle \left\{t_{e},q_{v}:e\in E^{1},v\in E^{0}\right\}}$ is a Cuntz-Krieger ${\displaystyle E}$-family in a C*-algebra ${\displaystyle A}$ there exists a ${\displaystyle *}$-homomorphism ${\displaystyle \phi :C^{*}(E)\to A}$ with ${\displaystyle \phi (s_{e})=t_{e}}$ for all ${\displaystyle e\in E^{1}}$ and ${\displaystyle \phi (p_{v})=q_{v}}$ for all ${\displaystyle v\in E^{0}}$. Existence of ${\displaystyle C^{*}(E)}$ for any graph ${\displaystyle E}$ was established by Kumjian, Pask, and Raeburn.^[3] Uniqueness of ${\displaystyle C^{*}(E)}$ (up to ${\displaystyle *}$-isomorphism) follows directly from the universal property.

Examples

The graph C*-algebra has been computed for many graphs. Conversely, for certain classes of C*-algebras it has been shown how to construct a graph whose C*-algebra is ${\displaystyle *}$-isomorphic or Morita equivalent to a given C*-algebra of that class.

The following table shows a number of directed graphs and their C*-algebras. We use the convention that a double arrow drawn from one vertex to another and labeled ${\displaystyle \infty }$ indicates that there are a countably infinite number of edges from the first vertex to the second.

Directed Graph ${\displaystyle E}$	Graph C*-algebra ${\displaystyle C^{*}(E)}$
	${\displaystyle \mathbb {C} }$, the complex numbers
	${\displaystyle C(\mathbb {T} )}$, the complex-valued continuous functions on the circle ${\displaystyle \mathbb {T} }$
	${\displaystyle M_{n}(\mathbb {C} )}$, the ${\displaystyle n\times n}$ matrices with entries in ${\displaystyle \mathbb {C} }$
	${\displaystyle {\mathcal {K}}}$, the compact operators on a separable infinite-dimensional Hilbert space
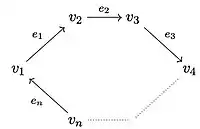	${\displaystyle M_{n}(C(\mathbb {T} ))}$, the ${\displaystyle n\times n}$ matrices with entries in ${\displaystyle C(\mathbb {T} )}$
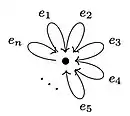	${\displaystyle {\mathcal {O}}_{n}}$, the Cuntz algebra generated by ${\displaystyle n}$ isometries
	${\displaystyle {\mathcal {O}}_{\infty }}$, the Cuntz algebra generated by a countably infinite number of isometries
	${\displaystyle {\mathcal {K}}^{1}}$, the unitization of the algebra of compact operators ${\displaystyle {\mathcal {K}}}$
	${\displaystyle {\mathcal {T}}}$, the Toeplitz algebra

The class of graph C*-algebras has been shown to contain various classes of C*-algebras. The C*-algebras in each of the following classes may be realized as graph C*-algebras up to ${\displaystyle *}$-isomorphism:

• Cuntz algebras
• Cuntz-Krieger algebras
• finite-dimensional C*-algebras
• stable AF algebras

The C*-algebras in each of the following classes may be realized as graph C*-algebras up to Morita equivalence:

• AF algebras^[6]
• Kirchberg algebras with free K₁-group

Correspondence between graph and C*-algebraic properties

One remarkable aspect of graph C*-algebras is that the graph ${\displaystyle E}$ not only describes the relations for the generators of ${\displaystyle C^{*}(E)}$, but also various graph-theoretic properties of ${\displaystyle E}$ can be shown to be equivalent to C*-algebraic properties of ${\displaystyle C^{*}(E)}$. Indeed, much of the study of graph C*-algebras is concerned with developing a lexicon for the correspondence between these properties, and establishing theorems of the form "The graph ${\displaystyle E}$ has a certain graph-theoretic property if and only if the C*-algebra ${\displaystyle C^{*}(E)}$ has a corresponding C*-algebraic property." The following table provides a short list of some of the more well-known equivalences.

Property of ${\displaystyle E}$	Property of ${\displaystyle C^{*}(E)}$
${\displaystyle E}$ is a finite graph.	${\displaystyle C^{*}(E)}$ is finite-dimensional.
The vertex set ${\displaystyle E^{0}}$ is finite.	${\displaystyle C^{*}(E)}$ is unital (i.e., ${\displaystyle C^{*}(E)}$ contains a multiplicative identity).
${\displaystyle E}$ has no cycles.	${\displaystyle C^{*}(E)}$ is an AF algebra.
${\displaystyle E}$ satisfies the following three properties: Condition (L), for each vertex ${\displaystyle v}$ and each infinite path ${\displaystyle \alpha }$ there exists a directed path from ${\displaystyle v}$ to a vertex on ${\displaystyle \alpha }$, and for each vertex ${\displaystyle v}$ and each singular vertex ${\displaystyle w}$ there exists a directed path from ${\displaystyle v}$ to ${\displaystyle w}$	${\displaystyle C^{*}(E)}$ is simple.
${\displaystyle E}$ satisfies the following three properties: Condition (L), for each vertex ${\displaystyle v}$ in ${\displaystyle E}$ there is a path from ${\displaystyle v}$ to a cycle.	Every hereditary subalgebra of ${\displaystyle C^{*}(E)}$ contains an infinite projection. (When ${\displaystyle C^{*}(E)}$ is simple this is equivalent to ${\displaystyle C^{*}(E)}$ being purely infinite.)

The gauge action

The universal property produces a natural action of the circle group ${\displaystyle \mathbb {T}$ :=\{z\in \mathbb {C} :|z|=1\}} on ${\displaystyle C^{*}(E)}$ as follows: If ${\displaystyle \left\{s_{e},p_{v}:e\in E^{1},v\in E^{0}\right\}}$ is a universal Cuntz-Krieger ${\displaystyle E}$-family, then for any unimodular complex number ${\displaystyle z\in \mathbb {T} }$, the collection ${\displaystyle \left\{zs_{e},p_{v}:e\in E^{1},v\in E^{0}\right\}}$ is a Cuntz-Krieger ${\displaystyle E}$-family, and the universal property of ${\displaystyle C^{*}(E)}$ implies there exists a ${\displaystyle *}$-homomorphism ${\displaystyle \gamma _{z}:C^{*}(E)\to C^{*}(E)}$ with ${\displaystyle \gamma _{z}(s_{e})=zs_{e}}$ for all ${\displaystyle e\in E^{1}}$ and ${\displaystyle \gamma _{z}(p_{v})=p_{v}}$ for all ${\displaystyle v\in E^{0}}$. For each ${\displaystyle z\in \mathbb {T} }$ the ${\displaystyle *}$-homomorphism ${\displaystyle \gamma _{\overline {z}}}$ is an inverse for ${\displaystyle \gamma _{z}}$, and thus ${\displaystyle \gamma _{z}}$ is an automorphism. This yields a strongly continuous action ${\displaystyle \gamma$ :\mathbb {T} \to \operatorname {Aut} C^{*}(E)} by defining ${\displaystyle \gamma (z):=\gamma _{z}}$. The gauge action ${\displaystyle \gamma }$ is sometimes called the canonical gauge action on ${\displaystyle C^{*}(E)}$. It is important to note that the canonical gauge action depends on the choice of the generating Cuntz-Krieger ${\displaystyle E}$-family ${\displaystyle \left\{s_{e},p_{v}:e\in E^{1},v\in E^{0}\right\}}$. The canonical gauge action is a fundamental tool in the study of ${\displaystyle C^{*}(E)}$. It appears in statements of theorems, and it is also used behind the scenes as a technical device in proofs.

The uniqueness theorems

There are two well-known uniqueness theorems for graph C*-algebras: the gauge-invariant uniqueness theorem and the Cuntz-Krieger uniqueness theorem. The uniqueness theorems are fundamental results in the study of graph C*-algebras, and they serve as cornerstones of the theory. Each provides sufficient conditions for a ${\displaystyle *}$-homomorphism from ${\displaystyle C^{*}(E)}$ into a C*-algebra to be injective. Consequently, the uniqueness theorems can be used to determine when a C*-algebra generated by a Cuntz-Krieger ${\displaystyle E}$-family is isomorphic to ${\displaystyle C^{*}(E)}$; in particular, if ${\displaystyle A}$ is a C*-algebra generated by a Cuntz-Krieger ${\displaystyle E}$-family, the universal property of ${\displaystyle C^{*}(E)}$ produces a surjective ${\displaystyle *}$-homomorphism ${\displaystyle \phi :C^{*}(E)\to A}$, and the uniqueness theorems each give conditions under which ${\displaystyle \phi }$ is injective, and hence an isomorphism. Formal statements of the uniqueness theorems are as follows:

The Gauge-Invariant Uniqueness Theorem: Let ${\displaystyle E}$ be a graph, and let ${\displaystyle C^{*}(E)}$ be the associated graph C*-algebra. If ${\displaystyle A}$ is a C*-algebra and ${\displaystyle \phi :C^{*}(E)\to A}$ is a ${\displaystyle *}$-homomorphism satisfying the following two conditions:

1. there exists a gauge action ${\displaystyle \beta$ :\mathbb {T} \to \operatorname {Aut} A} such that ${\displaystyle \phi \circ \beta _{z}=\gamma _{z}\circ \phi }$ for all ${\displaystyle z\in \mathbb {T} }$, where ${\displaystyle \gamma }$ denotes the canonical gauge action on ${\displaystyle C^{*}(E)}$, and
2. ${\displaystyle \phi (p_{v})\neq 0}$ for all ${\displaystyle v\in E^{0}}$,

then ${\displaystyle \phi }$ is injective.

The Cuntz-Krieger Uniqueness Theorem: Let ${\displaystyle E}$ be a graph satisfying Condition (L), and let ${\displaystyle C^{*}(E)}$ be the associated graph C*-algebra. If ${\displaystyle A}$ is a C*-algebra and ${\displaystyle \phi :C^{*}(E)\to A}$ is a ${\displaystyle *}$-homomorphism with ${\displaystyle \phi (p_{v})\neq 0}$ for all ${\displaystyle v\in E^{0}}$, then ${\displaystyle \phi }$ is injective.

The gauge-invariant uniqueness theorem implies that if ${\displaystyle \left\{s_{e},p_{v}:e\in E^{1},v\in E^{0}\right\}}$ is a Cuntz-Krieger ${\displaystyle E}$-family with nonzero projections and there exists a gauge action ${\displaystyle \beta }$ with ${\displaystyle \beta _{z}(p_{v})=p_{v}}$ and ${\displaystyle \beta _{z}(s_{e})=zs_{e}}$ for all ${\displaystyle v\in E^{0}}$, ${\displaystyle e\in E^{1}}$, and ${\displaystyle z\in \mathbb {T} }$, then ${\displaystyle \{s_{e},p_{v}:e\in E^{1},v\in E^{0}\}}$ generates a C*-algebra isomorphic to ${\displaystyle C^{*}(E)}$. The Cuntz-Krieger uniqueness theorem shows that when the graph satisfies Condition (L) the existence of the gauge action is unnecessary; if a graph ${\displaystyle E}$ satisfies Condition (L), then any Cuntz-Krieger ${\displaystyle E}$-family with nonzero projections generates a C*-algebra isomorphic to ${\displaystyle C^{*}(E)}$.

Ideal structure

The ideal structure of ${\displaystyle C^{*}(E)}$ can be determined from ${\displaystyle E}$. A subset of vertices ${\displaystyle H\subseteq E^{0}}$ is called hereditary if for all ${\displaystyle e\in E^{1}}$, ${\displaystyle s(e)\in H}$ implies ${\displaystyle r(e)\in H}$. A hereditary subset ${\displaystyle H}$ is called saturated if whenever ${\displaystyle v}$ is a regular vertex with ${\displaystyle \{r(e):e\in E^{0},s(e)=v\}\subseteq H}$, then ${\displaystyle v\in H}$. The saturated hereditary subsets of ${\displaystyle E}$ are partially ordered by inclusion, and they form a lattice with meet ${\displaystyle H_{1}\wedge H_{2}:=H_{1}\cap H_{2}}$ and join ${\displaystyle H_{1}\vee H_{2}}$ defined to be the smallest saturated hereditary subset containing ${\displaystyle H_{1}\cup H_{2}}$.

If ${\displaystyle H}$ is a saturated hereditary subset, ${\displaystyle I_{H}}$ is defined to be closed two-sided ideal in ${\displaystyle C^{*}(E)}$ generated by ${\displaystyle \{p_{v}:v\in H\}}$. A closed two-sided ideal ${\displaystyle I}$ of ${\displaystyle C^{*}(E)}$ is called gauge invariant if ${\displaystyle \gamma _{z}(a)\in C^{*}(E)}$ for all ${\displaystyle a\in I}$ and ${\displaystyle z\in \mathbb {T} }$. The gauge-invariant ideals are partially ordered by inclusion and form a lattice with meet ${\displaystyle I_{1}\wedge I_{2}:=I_{1}\cap I_{2}}$ and joint ${\displaystyle I_{1}\vee I_{2}}$ defined to be the ideal generated by ${\displaystyle I_{1}\cup I_{2}}$. For any saturated hereditary subset ${\displaystyle H}$, the ideal ${\displaystyle I_{H}}$ is gauge invariant.

The following theorem shows that gauge-invariant ideals correspond to saturated hereditary subsets.

Theorem: Let ${\displaystyle E}$ be a row-finite graph. Then the following hold:

1. The function ${\displaystyle H\mapsto I_{H}}$ is a lattice isomorphism from the lattice of saturated hereditary subsets of ${\displaystyle E}$ onto the lattice of gauge-invariant ideals of ${\displaystyle C^{*}(E)}$ with inverse given by ${\displaystyle I\mapsto \left\{v\in E^{0}:p_{v}\in I\right\}}$.
2. For any saturated hereditary subset ${\displaystyle H}$, the quotient ${\displaystyle C^{*}(E)/I_{H}}$ is ${\displaystyle *}$-isomorphic to ${\displaystyle C^{*}(E\setminus H)}$, where ${\displaystyle E\setminus H}$ is the subgraph of ${\displaystyle E}$ with vertex set ${\displaystyle (E\setminus H)^{0}:=E^{0}\setminus H}$ and edge set ${\displaystyle (E\setminus H)^{1}:=E^{1}\setminus r^{-1}(H)}$.
3. For any saturated hereditary subset ${\displaystyle H}$, the ideal ${\displaystyle I_{H}}$ is Morita equivalent to ${\displaystyle C^{*}(E_{H})}$, where ${\displaystyle E_{H}}$ is the subgraph of ${\displaystyle E}$ with vertex set ${\displaystyle E_{H}^{0}:=H}$ and edge set ${\displaystyle E_{H}^{1}:=s^{-1}(H)}$.
4. If ${\displaystyle E}$ satisfies Condition (K), then every ideal of ${\displaystyle C^{*}(E)}$ is gauge invariant, and the ideals of ${\displaystyle C^{*}(E)}$ are in one-to-one correspondence with the saturated hereditary subsets of ${\displaystyle E}$.

Desingularization

The Drinen-Tomforde Desingularization, often simply called desingularization, is a technique used to extend results for C*-algebras of row-finite graphs to C*-algebras of countable graphs. If ${\displaystyle E}$ is a graph, a desingularization of ${\displaystyle E}$ is a row-finite graph ${\displaystyle F}$ such that ${\displaystyle C^{*}(E)}$ is Morita equivalent to ${\displaystyle C^{*}(F)}$.^[7] Drinen and Tomforde described a method for constructing a desingularization from any countable graph: If ${\displaystyle E}$ is a countable graph, then for each vertex ${\displaystyle v_{0}}$ that emits an infinite number of edges, one first chooses a listing of the outgoing edges as ${\displaystyle s^{-1}(v_{0})=\{e_{0},e_{1},e_{2},\ldots \}}$, one next attaches a tail of the form

to ${\displaystyle E}$ at ${\displaystyle v_{0}}$, and finally one erases the edges ${\displaystyle e_{0},e_{1},e_{2},\ldots }$ from the graph and redistributes each along the tail by drawing a new edge ${\displaystyle f_{i}}$ from ${\displaystyle v_{i}}$ to ${\displaystyle r(e_{i})}$ for each ${\displaystyle i=0,1,2,\ldots }$.

Here are some examples of this construction. For the first example, note that if ${\displaystyle E}$ is the graph

then a desingularization ${\displaystyle F}$ is given by the graph

For the second example, suppose ${\displaystyle E}$ is the ${\displaystyle {\mathcal {O}}_{\infty }}$ graph with one vertex and a countably infinite number of edges (each beginning and ending at this vertex). Then a desingularization ${\displaystyle F}$ is given by the graph

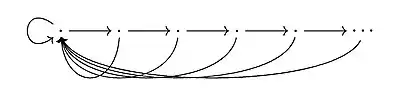
Desingularization has become a standard tool in the theory of graph C*-algebras,^[8] and it can simplify proofs of results by allowing one to first prove the result in the (typically much easier) row-finite case, and then extend the result to countable graphs via desingularization, often with little additional effort.

The technique of desingularization may not work for graphs containing a vertex that emits an uncountable number of edges. However, in the study of C*-algebras it is common to restrict attention to separable C*-algebras. Since a graph C*-algebra ${\displaystyle C^{*}(E)}$ is separable precisely when the graph ${\displaystyle E}$ is countable, much of the theory of graph C*-algebras has focused on countable graphs.

K-theory

The K-groups of a graph C*-algebra may be computed entirely in terms of information coming from the graph. If ${\displaystyle E}$ is a row-finite graph, the vertex matrix of ${\displaystyle E}$ is the ${\displaystyle E^{0}\!\times \!E^{0}}$ matrix ${\displaystyle A_{E}}$ with entry ${\displaystyle A_{E}(v,w)}$ defined to be the number of edges in ${\displaystyle E}$ from ${\displaystyle v}$ to ${\displaystyle w}$. Since ${\displaystyle E}$ is row-finite, ${\displaystyle A_{E}}$ has entries in ${\displaystyle \mathbb {N} \cup \{0\}}$ and each row of ${\displaystyle A_{E}}$ has only finitely many nonzero entries. (In fact, this is where the term "row-finite" comes from.) Consequently, each column of the transpose ${\displaystyle A_{E}^{t}}$ contains only finitely many nonzero entries, and we obtain a map ${\textstyle A_{E}^{t}:\bigoplus _{E^{0}}\mathbb {Z} \to \bigoplus _{E^{0}}\mathbb {Z} }$ given by left multiplication. Likewise, if ${\displaystyle I}$ denotes the ${\displaystyle E^{0}\!\times \!E^{0}}$ identity matrix, then ${\textstyle I-A_{E}^{t}:\bigoplus _{E^{0}}\mathbb {Z} \to \bigoplus _{E^{0}}\mathbb {Z} }$ provides a map given by left multiplication.

Theorem: Let ${\displaystyle E}$ be a row-finite graph with no sinks, and let ${\displaystyle A_{E}}$ denote the vertex matrix of ${\displaystyle E}$. Then

$${\displaystyle I-A_{E}^{t}:\bigoplus _{E^{0}}\mathbb {Z} \to \bigoplus _{E^{0}}\mathbb {Z} }$$

gives a well-defined map by left multiplication. Furthermore,

$${\displaystyle K_{0}(C^{*}(E))\cong \operatorname {coker} (I-A_{E}^{t})\quad {\text{ and }}\quad K_{1}(C^{*}(E))\cong \ker(I-A_{E}^{t}).}$$

In addition, if ${\displaystyle C^{*}(E)}$ is unital (or, equivalently, ${\displaystyle E^{0}}$ is finite), then the isomorphism ${\displaystyle K_{0}(C^{*}(E))\cong \operatorname {coker} (I-A_{E}^{t})}$ takes the class of the unit in ${\displaystyle K_{0}(C^{*}(E))}$ to the class of the vector ${\displaystyle (1,1,\ldots ,1)}$ in ${\displaystyle \operatorname {coker} (I-A_{E}^{t})}$.

Since ${\displaystyle K_{1}(C^{*}(E))}$ is isomorphic to a subgroup of the free group ${\textstyle \bigoplus _{E^{0}}\mathbb {Z} }$, we may conclude that ${\displaystyle K_{1}(C^{*}(E))}$ is a free group. It can be shown that in the general case (i.e., when ${\displaystyle E}$ is allowed to contain sinks or infinite emitters) that ${\displaystyle K_{1}(C^{*}(E))}$ remains a free group. This allows one to produce examples of C*-algebras that are not graph C*-algebras: Any C*-algebra with a non-free K₁-group is not Morita equivalent (and hence not isomorphic) to a graph C*-algebra.

Notes