Gun dynamics encompasses aspects of gun technology, such as recoil and impact. In the 1970s, the introduction of the United States Army Symposium on Gun Dynamics[1][2][3][4][5] defined it as the study of internal ballistics that are unrelated to propellants and combustion. In particular, it is concerned with the interactive dynamics between the projectile, barrel, and mounting, and the effect that they have on the accuracy and consistency of the gun.

Gun designers realized that there may be an interaction between the barrel and the shot that was likely to affect accuracy and consistency. It is only since the 1970s that the ability to compute the motion has become practical. If a perfectly straight barrel was fired in zero gravity, the barrel recoiled along its central axis with no off axis forces, the shot was perfectly balanced and a perfect fit within the barrel, and all the forces were symmetrical, then the shot should exit the barrel in the direction in which the muzzle was initially pointing. In practice none of these conditions can be met, and inevitably some transverse vibration is introduced to the barrel and the shot. This results in shot jump, where the trajectory of the shot does not correspond with the initial direction of the muzzle.[6]

Gun dynamics describes the physical causes of barrel and shot vibration, and the effect they may have on accuracy and consistency. These motions are predicted using theoretical methods and mathematical modelling techniques, and experimental techniques which can be used to measure some of the phenomena which result.[7][8][9]

Accuracy and consistency

When a gun is aimed so that its muzzle is pointing at a specific point (the point of aim) on a flat target perpendicular to the muzzle face. When the gun, is fired the shot hits a point P on the target. The distance between point A and P is sometimes referred to as an indication of the precision of the weapon.[7]

Figure 1: Good and bad consistency

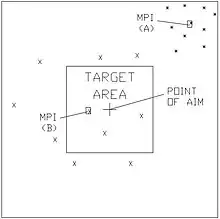
Subsequent rounds are unlikely to hit point P, and a pattern of hits will emerge after many rounds. The average of the points of impact of all the individual rounds is called the Mean Point of Impact (MPI).[10] The dispersion about an MPI provides a measure of the consistency and is often given in terms of the standard deviation.[7]

The situation is complicated by the fact that if 10 rounds are fired, the MPI derived from those rounds may differ from a further 10 rounds fired on another occasion. The distribution of the MPI between occasions provides a measure of the accuracy. This may be complicated even more when a complete weapon system is considered, and the MPI is found to vary for (as an example) different barrels of the same type.

Figures 1 to 3 demonstrate the results for guns with good and bad accuracy and consistency.

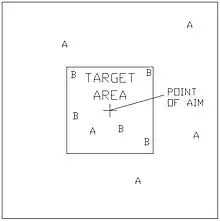
Figure 2: The mean points of impact for guns A and B (case 1)

In Figure 1, two guns have been fired, each with a set of 10 shots. The position of the shots on the target from gun A are shown as asterisks (*), and from gun B as Xs. The spread of shots from gun A is much smaller than those for gun B. Also, the MPI of A is off the target area, whereas that of B is on the target area. Figure 2 shows the MPIs of the two guns for five serials fired from each gun on different occasions. All the MPIs of gun B are on the target area, whereas those of gun A are well spread. The conclusion in this case is that gun A has good consistency, but poor accuracy. Gun B has poor consistency, but good accuracy.

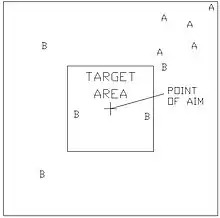
Figure 3: The mean points of impact for guns A and B (case 2)

A more realistic possibility is shown in Figure 3. In this case, assuming that each serial had the same consistency as those shown in Figure 1, gun A shows good consistency and accuracy, and gun B is poor on both counts. The fact that the MPIs of gun A are not on the target can be corrected for in the sighting. However, if this was a tank gun and the MPIs were very different for different tanks, then the users of the tanks may find this unacceptable. This is because finding a correction value for each tank by 'shooting in' can be very costly with modern ammunition.

When considering the chance of hitting a target with the first round fired, both accuracy and consistency must be taken into account. Figure 4 categorizes the sources of error for a tank gun which may affect its ability to hit the target.[7]

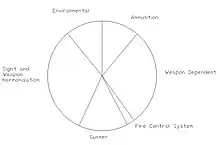
Figure 4: The major elements of a tank system error budget

The sources of error are broken down as follows:

  • The gunner will affect the consistency, as his ability to perform from one round to the next will change.
  • The sight and weapon harmonization will affect the occasion-to-occasion MPI. This may be because of simple maintenance, although more complex reasons have been shown to occur in certain systems.
  • Environmental conditions will both affect consistency (e.g. variable wind conditions down range), or accuracy (e.g. change in temperature and hence air density which affects the external trajectory). In some cases, these are accountable and could possibly be corrected in the fire control system.
  • The ammunition, both the charge and the shot, will suffer from manufacturing tolerances which has an effect on consistency.
  • The weapon-dependent parameters, such as the straightness of the barrel or the clearance in the bearings, will have an effect on both consistency and accuracy. As an example, when the barrel temperature rises and the bearing clearances change, the jump of the shot will change. This will affect the consistency. Similarly, the straightness of the barrel will affect the final trajectory, and hence the accuracy, but it may also affect the shot pitch velocity at launch, which in turn may affect the consistency.
  • The fire control system should represent a small part of the error budget.

The effects of external ballistics are ignored in this context, and only effects which occur while the shot is in the barrel are considered. Hence, the interest will be in the weapon dependent part of the error budget, together with the part of the ammunition segment which affects the dynamics of the shot in the bore. Even so, some of the launch parameters may still contribute to what occurs after the shot has left the barrel. In particular, the yaw angle and angular velocity will affect stabilization and aerodynamics following launch.[7]

Barrel and shot jump

The shot will not necessarily hit the point of aim. In practice, a gunner will aim a gun with reference to the trajectory of the shot. The gravitational and aerodynamic effects including drag can be calculated and the initial pointing angle of the muzzle adjusted accordingly. A further adjustment then must be made for the difference between the calculated point of impact and the actual anticipated point of impact. This difference will normally be a known value obtained from initial development of the gun, and is usually given the term 'gun jump'. It is caused by the fact that the trajectory of the shot as it leaves the gun may not be the same as the initial pointing direction of the muzzle. There may also be further external ballistic effects which may in themselves be a function of the launch parameters of the shot. The components of gun jump are shown in Figure 5.

Figure 5. The components of gun jump

When a gun is fired, the angle of the muzzle changes, and there is a transverse velocity component of the muzzle. If the shot followed the center-line of the bore exactly, then the difference in initial trajectory of the shot compared to the initial pointing angle of the muzzle would be equal to the change of muzzle angle plus its transverse velocity component divided by the shot velocity relative to the muzzle at exit. This may be referred to as barrel jump. In the case of a perfectly fitting non-spinning solid ball, this would compose all of the gun jump.

In practice, the shot is bouncing relative to the barrel. Adding this to barrel jump results in shot jump. In this case, it is the difference between the initial pointing direction of the muzzle and the final trajectory of the center of gravity of the shot as it leaves the barrel.

After the shot leaves the muzzle, there will be aerodynamic effects which modify the trajectory. Adding these to shot jump results in total gun jump.[11]

Mechanisms producing shot jump

Introduction

When a gun is fired it recoils and various forces are introduced which cause the barrel and shot to move in a direction perpendicular to the axis of the barrel.[12][13][14] The shot may also have angular displacements about axes perpendicular to its longitudinal axis. Shot pitch is defined as angular displacement about a horizontal axis perpendicular to the barrel axis. Shot yaw is defined as angular displacements about a vertical axis perpendicular to the barrel axis.[7]

There is an interaction between the shot and the barrel such that each affects the motion of the other. Factors cause the barrel to vibrate independently of and due to the shot.

Off-axis masses

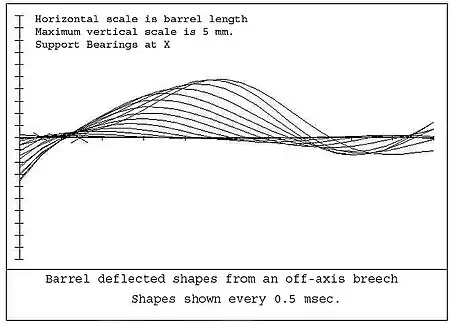
Figure 6: The effect of an off-axis breech on barrel motion

Most guns have the center of gravity of the total recoiling mass offset from the center-line of the bore. This is normally caused by specific components which are asymmetric.

As an example, in most tank guns the center of gravity of the breech is normally below the barrel axis. Therefore, when the barrel recoils the inertial force from the breech produces a moment on the rear end of the barrel. This causes a wave to travel down the barrel which quickly overtakes the shot and results in a deflection of the muzzle before shot exit. Figure 6 shows the typical response of a tank gun barrel for an off-axis breech. Each line represents the shape that the barrel takes up at 0.5 millisecond intervals. These curves were produced by a simulation of an actual system.

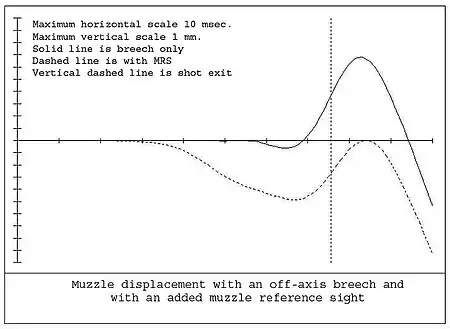
Figure 7: Muzzle displacement with breech and with or without MRS

Another off axis component found on some tank guns is a muzzle reference sight (MRS). As the muzzle recoils, the moment produced by the inertial force on the muzzle reference sight causes the muzzle to move downwards. In this case, the barrel does not recoil as a solid mass. In practice the barrel lengthens, and a longitudinal wave travels up the barrel. The muzzle does not therefore move backwards at the same time as the breech and the time delay can be significant on the effect of the muzzle reference sight. However, the longitudinal wave travels faster than the bending wave along the barrel. Therefore, the transverse motion caused by the off-axis muzzle reference sight occurs before the wave from the breech gets there. Figure 7 shows a plot of muzzle motion caused by an off-axis breech, and a second curve with an added muzzle reference sight.

Any off-axis masses can affect the barrel motion. In the case of asymmetrical barrels, the fact that the center of mass of the barrel sections may not coincide with the principal bending axes is also significant.

Barrel curvature

A curved barrel in recoil is similar to a straight barrel with off-axis masses: as the barrel recoils it will try to straighten.[15] Even if the barrel is straight with no off-axis masses, if the recoil axis is not parallel to the barrel axis then the same argument will apply. Generally, when compared to the effect of the breech, the result on muzzle and shot motion is small.

Barrel expansion

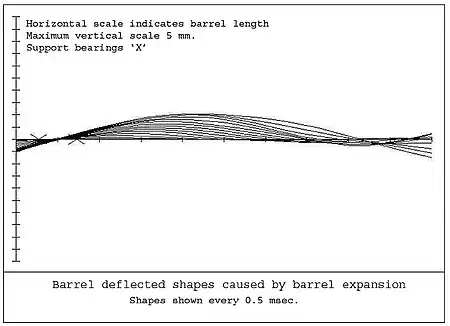
Figure 8: The effect of barrel expansion on barrel motion

When a gun is fired, the barrel expands. For example, in a tank gun, the barrel normally sits on bearings, which have clearances. When the gun is fired, the barrel expands, causing movement within the bearings. When the center of gravity of the total recoiling mass is ahead of the front bearing, at rest, the barrel sits on the bottom of the front bearing and pushes up against the top of the rear bearing. When fired, barrel expansion causes the barrel to push up against the front bearing and down against the rear bearing, causing the barrel to flex. A typical response is shown in Figure 8. If the center of gravity is between the bearings, a similar case will arise, but the final response will be modified. When a bearing is ahead of the shot start position, the expansion is delayed until the shot moves past the bearing.

This phenomenon is difficult to measure and separate from other vibration producing mechanisms. However, simulations show that the result can significantly modify the barrel motion.[16]

Off-axis forces

Apart from off-axis inertial forces and barrel expansion, there are often a number of other possible causes of additional off-axis forces.

The most obvious of these may be an offset buffer or recuperator. In this case they will produce a force which acts at a distance from the barrel axis, and hence produce a moment. Even if there are two buffers which are expected to act evenly on either side of the barrel, bad maintenance or wear may cause them to have different characteristics. In this case a moment will be produced which will cause the barrel to vibrate. A particularly extreme case would be a single combined buffer and recuperator which acts to one side of the barrel. This would cause lateral vibration of the barrel and produce different horizontal jump characteristics for different muzzle velocities. The fire control system would therefore have to modify the azimuth as well as the elevation for different charges and shot types.

Depending upon the type of gun and its application, there may be other possible sources of external forces. Friction in bearings at start of recoil may be significant, and repeat fire weapons can be affected by shot ejection or a muzzle brake.

Shot interaction

If the barrel moves, it is reasonable to assume that the shot moves with the barrel. Earlier research work assumed that the shot followed the motion of the barrel exactly, and that the shot had little to no effect on the barrel motion. In practice the shot can move relative to the barrel and can bounce and pitch or yaw within the bore.[17][18] The forces which the shot can exert on the barrel can be very large. These are caused by out of balance forces on the shot plus reactive forces as the shot is forced to follow the curved shape of the barrel.

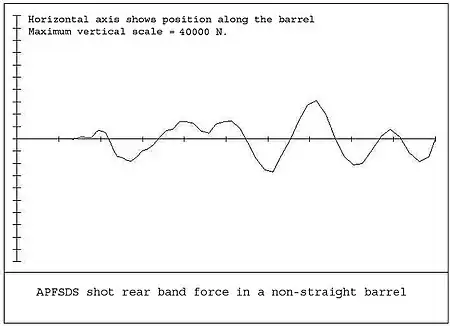
Figure 9: Typical transverse forces on a shot rear band

As an example, consider a shot which has its center of mass slightly displaced from the geometrically central axis. In this case if the shot is spun by the rifling about its geometric axis, a centrifugal force will be generated which will affect the barrel. For example, a shot mass of 10 kilograms (22 lb) with an offset of 0.1 mm and spin velocity of 500 cycles/sec will generate a force of 9870 N.[6]

In another case assume that a non-straight barrel has a radius of curvature of 1000 m, which is a relatively straight barrel. If the shot mass is 10 kg and its velocity is 1000 m/s, the force generated by the shot on the side of the barrel, as it tries to follow this curvature, will be 10,000 N.

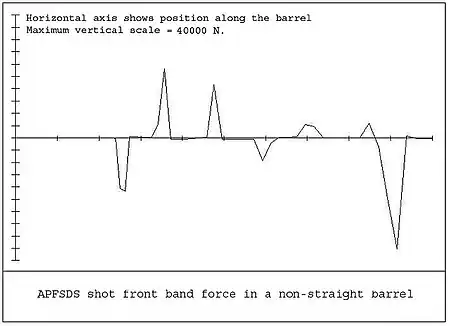
Figure 10: Typical transverse forces on a shot front band

Thus, transverse forces generated between the shot and the barrel may be very large. In reality there is some elasticity and clearance between the shot and the barrel. The shot motion therefore becomes very complex, particularly if it is spinning and gyroscopic forces are also included. Figures 9 and 10 show the typical theoretical forces for the rear band and the front band of a 120mm APFSDS shot. These vary considerably depending on barrel straightness, shot band stiffness, pressure, time curve, and other factors.

Only a number of the points have been plotted and the curves would be expected to be smoother. In the case of the front band, there are times when the force is zero. This is because of the clearance between the band and the barrel, and the forces appear to be more like impacts. In the case of long flexible projectiles, the above forces may cause bending of the projectile. This adds even more complication to the situation.

Cradle and mounting effects

The mounting of the barrel can also have a significant effect on the motion of the barrel when it is fired. In a tank gun the mounting is normally in a structure called the 'cradle' which is supported in bearings usually referred to as trunnions which enable elevation of the gun. Mountings of other gun systems can vary considerably, but in all cases the mounting can affect barrel motion considerably.[19][20]

Theoretical simulation

Introduction

The main aim of a theoretical simulation of the dynamics of the barrel, mounting, and shot, is to predict the sensitivity of the shot exit conditions to variations in the gun system parameters. This will then assist the gun designer to produce suitable designs and keep manufacturing tolerances within reasonable limits, while maintaining good dispersion and accuracy. A secondary result of such simulations is that further information is made available which can assist in the design process. For example, the prediction of shot band forces, or the bending stresses in long rod penetrators, gives added confidence to the strength of design process. Simulations in a single plane (2 dimensional) can be used to give limited appreciation with certain systems, but for a full understanding a full 3-dimensional analysis is important.

In a simulation, the main components are the barrel and shot which interact with one another. Other components, such as the mounting or the buffers, will be able to interact with the barrel, and any mathematical model should take this into account. As with any dynamic model it is easiest to treat each component separately, and derive equations of motion which are general enough to allow changes in the system to be made easily.

The following list shows many of the parameters which are normally included in a typical simulation:

  • Barrel: Material density, elastic modulus, length, profile or cross-section, curvature, wear, smooth or rifled bores, expansion, added masses
  • Added forces: bearings, buffers, recuperators, gas forces, shot reactions
  • Mounting and cradle: bearing stiffnesses, bearing clearances, mass and inertia, flexibility, trunnion position, elevation gear stiffness, and elevation gear backlash
  • Added forces: barrel reactions via the bearings, buffers, and recuperators
  • Shot: mass, inertia, clearances, bounce and pitch natural frequencies, flexibility, applied gas forces, and reaction forces with the barrel

Barrel

The barrel can normally be considered a flexible tube, which for dynamic analysis is a multi-degree of freedom system. There are two distinct techniques which have been used in gun dynamics for mathematically modelling this. The first is a direct integration of the beam equations by a finite difference technique. The RAMA program, named after the Richtmyer and Morton's Algorithm that it used, was based on this technique.[12] The second is by using the finite element technique. A number of programs have been written using this method including SIMBAD,[13][21][22] DYNACODE,[5] and the Little Rascal.[23]

In both methods researchers have concentrated on the use of Euler-Bernoulli theory for the beam equations,[24] but in some cases Timoshenko beam theory is considered more appropriate, particularly where shear deformations are anticipated to be significant. Although not discussed here, in exceptional cases a finite element analysis using brick elements for the barrel and the shot has been made. This gives considerably more information than is normally required, including stress information across the thickness of the barrel wall. In this case, the program runtime for a single round from a 120 mm tank gun can exceed many hours.

Shot

The solution of the barrel equations produces displacements, velocities, and accelerations at points on the barrel in the global directions defined by fixed axes. It is therefore important that any shot model should relate to these same directions. In the case of a simple single plane simulation (2 dimensional) the same axes can be used directly in the shot analysis. In a full analysis (3 dimensional) although the translation of the shot center of gravity can be analyzed directly in the global directions, it is preferable for the angular motion to be defined relative to axes attached to the shot. This then enables Euler's dynamical equations to be applied directly. A transformation from the shot's own axes to the global axes then has to be made.

The contact between the shot and the barrel must also be simulated. It is normally assumed that contact is made through two points on the shot (the shot bands). Each band force is then composed of a stiffness term, which might include both a linear and a moment stiffness,[25] plus a damping term. These are then functions of the respective displacements and velocities of the bands relative to the barrel. Clearances must also be simulated. It is therefore important that displacements and velocities of the shot relative to the barrel be calculated accurately. The base pressure must also be included.

If the barrel is rifled, the driving torque on the shot provided by the rifling is derived by assuming a torsional stiffness of the rear driving band, plus a viscous damping term. The stiffness need not necessarily be linear, as long as it is assumed that the torque is some function of the relative displacements between the shot and the barrel.

If the shot center of gravity is offset from its geometric center, this will produce two main effects. First the gas pressure on the rear of the shot will produce a moment about the center of gravity. Second, as the shot is spun by the rifling it will exert a centrifugal force on the side of the barrel.

In a simulation, the shot pitch and yaw needs to be defined. In a two dimensional simulation, purely in the OXY plane, the definition of shot pitch would be fairly obvious. In a three dimensional analysis the definition needs to be more explicit. This is because the shot Oy and Oz axes no longer remain aligned in the global directions. A definition of angular displacement about axes attached to the shot would therefore be difficult to understand. However it is necessary to define some angular displacements which can be used to define the displacements of the shot relative to the barrel as discussed earlier.

The simulation becomes even more complicated when shots with flexibility are considered. Examples of this are long rod penetrators used in FSDS rounds.[26][27][28]

In a practical simulation of the shot, the steps would be as follows:

  1. Locate the position of the shot rear and front bands along the barrel.
  2. Calculate the deflections of the barrel at the band positions.
  3. Find the deflections of the bands.
  4. Use the band deflections to produce forces in the global directions
  5. Find the twist of the driving band and derive the torque in the global directions.
  6. Apply derived forces to the barrel.
  7. Apply linear forces to the shot.
  8. Transform forces (moments) to the shot axes directions.
  9. Apply transformed forces to the shot using Euler's dynamical equations.
  10. Update the transformation matrix.
  11. Calculate new pitch and yaw angles.

References

  1. ↑ T E Simkins, Parametric Resonance in Gun Tubes. First Conference on Dynamics of Precision Gun Weapons. R-TR-77-008, US Army Armament Research and Development Command, Dover, New Jersey, January 1977.
  2. ↑ T E Simkins, Transverse Response of Gun Tubes to Curvature Induced Loads. Second US Army Symposium on Gun Dynamics, 19–22 September 1978.
  3. ↑ B A Taylor and P G Thomasson, A Consistent R and D Assessment Technique for the Modelling of Gun System Dynamics. Third US Army Symposium on Gun Dynamics, 11–14 May 1982.
  4. ↑ T. F. Erline, M. D. Kregel. Modelling Gun Dynamics with Dominant Loads. 5th. US Army Symposium on Gun Dynamics, Rensselaerville, NY. 23–25 September 1987.
  5. 1 2 M. T. Soifer, R. S. Becker. DYNACODE-G/P and its Application to the 120mm Tank Gun. 5th. US Army Symposium on Gun Dynamics, Rensselaerville, NY. 23–25 September 1987.
  6. 1 2 D. N. Bulman. A comparison of theoretical jump for rifled and non rifled barrels. 5th US Army Symposium on Gun Dynamics, Rensselaerville NY, 23-25 Sept 87.
  7. 1 2 3 4 5 6 Textbook of Ballistics and Gunnery, London, Her Majesty’s Stationery Office
  8. ↑ G. Barker, A. E. Chambers, D. N. Bulman. An Accelerometer Technique for Measurement of Gun Muzzle Motion.  Presented to 6th US Symposium on Gun Dynamics, Tamiment, Pennsylvania, 14–17 May 1990
  9. ↑ D. N. Bulman, J. B. Hoyle. Accelerometers and their use for Measuring Transverse Motion of Gun Barrels. 5th International Symposium on Ballistics, Jerusalem, 21–24 May 1995.
  10. ↑ "mean point of impact (US DoD Definition)". www.militaryfactory.com. Retrieved 2023-10-06.
  11. ↑ E M Schmidt, "Analysis of Sources of Firing Error." 9th International Symposium on Ballistics, UK, 29 April to 1 May 1986.
  12. 1 2 S. E. Powell, P. G. H. Penny. The Theoretical Modelling of the Dynamics of Initially Non-straight Barrels using Finite Difference Techniques. 6th. US Army Symposium on Gun Dynamics, Rensselaerville, NY. 23–25 September 1987.
  13. 1 2 D. N. Bulman. Simulation of Gun Dynamics to Improve Accuracy and Consistency. 15th International Symposium on Ballistics, Jerusalem, Israel. 21–24 May 1995
  14. ↑ T E Simkins, Resonance of Flexural Waves in Gun Tubes. 5th US Army Symposium on Gun Dynamics, 23–25 September 1987.
  15. ↑ D. N. Bulman. The Effects of Barrel Droop on Gun Barrel Response. 9th International Symposium on Ballistics. RMCS, Shrivenham, UK, 29 April-1 May 1986
  16. ↑ D. N. Bulman. The Effect of Bearing Clearance and Barrel Expansion on Barrel Response. 4th US Army Gun Dynamics Symposium, Florida, 7–9 May 1985.
  17. ↑ G. Barker. An Experimental Investigation into In-bore Yaw in a Rifled Barrel using the RMCS Air Powered Gun. 5th. US Army Symposium on Gun Dynamics, Rensselaerville, NY. 23–25 September 1987
  18. ↑ P.W.W.Fuller. Measurement of Yaw In-bore. 5th International Symposium on Ballistics. Toulouse, 1980.
  19. ↑ D. N. Bulman, J. B. Hoyle. "A Comparison of Theoretical and Experimental Results with Regard to the Effects of Gun Cradle Design on Barrel and Shot Motion." 6th US Symposium on Gun Dynamics, Tamiment, Pennsylvania, 14–17 May 1990.
  20. ↑ D. N. Bulman, S. E. Powell. "The Theoretical Modelling of the Effect of Cradle Flexibility on Gun Barrel Response during the Firing Phase." 11th International Symposium on Ballistics, Brussels, 9–11 May 1989.
  21. ↑ D. N. Bulman, J. B. Hoyle. An experimental Validation of the SIMBAD Gun Dynamics simulation Package for Flexible Saboted Long Rod Projectiles. 7th US Symposium on Gun Dynamics, Newport, Rhode Island, 11–13 May 1993.
  22. ↑ SIMBAD (Simulation of Barrel Dynamics) User Manual (November 2000), Danby Engineering Ltd
  23. ↑ T. F. Erline, M. D. Kregel. Flexible Projectile Modelling using the Little Rascal Gun Dynamics Program. 6th US Symposium on Gun Dynamics, Tamiment, Pennsylvania, 14–17 May 1990
  24. ↑ D. A. Hopkins. Modelling Gun Dynamics with Three-Dimensional Beam Elements. 6th US Symposium on Gun Dynamics, Tamiment, Pennsylvania, 14–17 May 1990
  25. ↑ E. M. Patton. "Projectile Foundation Moment Generation." 4th US Army Gun Dynamics Symposium, Florida, 7–9 May 1985
  26. ↑ D. N. Bulman. "The In-bore Bending Dynamics of Long Rod Projectiles." 13th International Symposium on Ballistics, Stockholm, 1–3 June 1992
  27. ↑ D N Bulman, "The Introduction of Spin to an Existing Flexible Shot Model within a Gun Dynamics Simulation." 9th US Symposium on Gun Dynamics, 17–19 November 1998.
  28. ↑ D. A Rabern, K. A. Bannester. "Finite Elements Models to Predict the Structural Response of 120 mm Sabot/Rods During Launch." 6th. US Army Symposium on Gun Dynamics, Tamiment, Pennsylvania, 15–17 May 1990
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.