Icositruncated dodecadodecahedron
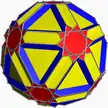Type	Uniform star polyhedron
Elements	F = 44, E = 180 V = 120 (χ = −16)
Faces by sides	20{6}+12{10}+12{10/3}
Coxeter diagram
Wythoff symbol	3 5 5/3 |
Symmetry group	Ih, [5,3], *532
Index references	U45, C57, W84
Dual polyhedron	Tridyakis icosahedron
Vertex figure	6.10.10/3
Bowers acronym	Idtid

3D model of an icositruncated dodecadodecahedron

In geometry, the icositruncated dodecadodecahedron or icosidodecatruncated icosidodecahedron is a nonconvex uniform polyhedron, indexed as U₄₅.

Convex hull

Its convex hull is a nonuniform truncated icosidodecahedron.

Truncated icosidodecahedron

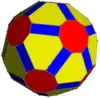Convex hull

Icositruncated dodecadodecahedron

Cartesian coordinates

Cartesian coordinates for the vertices of an icositruncated dodecadodecahedron are all the even permutations of

$${\displaystyle {\begin{array}{crrlc}{\Bigl (}&\pm {\bigl [}2-{\frac {1}{\varphi }}{\bigr ]},&\pm \,1,&\pm {\bigl [}2+\varphi {\bigr ]}&{\Bigr )},\\{\Bigl (}&\pm \,1,&\pm \,{\frac {1}{\varphi ^{2}}},&\pm {\bigl [}3\varphi -1{\bigr ]}&{\Bigr )},\\{\Bigl (}&\pm \,2,&\pm \,{\frac {2}{\varphi }},&\pm \,2\varphi &{\Bigr )},\\{\Bigl (}&\pm \,3,&\pm \,{\frac {1}{\varphi ^{2}}},&\pm \,\varphi ^{2}&{\Bigr )},\\{\Bigl (}&\pm \,\varphi ^{2},&\pm \,1,&\pm {\bigl [}3\varphi -2{\bigr ]}&{\Bigr )},\end{array}}}$$

where ${\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}$ is the golden ratio.

Related polyhedra

Tridyakis icosahedron

Tridyakis icosahedron
Type	Star polyhedron
Face
Elements	F = 120, E = 180 V = 44 (χ = −16)
Symmetry group	Ih, [5,3], *532
Index references	DU45
dual polyhedron	Icositruncated dodecadodecahedron

The tridyakis icosahedron is the dual polyhedron of the icositruncated dodecadodecahedron. It has 44 vertices, 180 edges, and 120 scalene triangular faces.

See also

• Catalan solid Duals to convex uniform polyhedra
• Uniform polyhedra
• List of uniform polyhedra

References

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208 Photo on page 96, Dorman Luke construction and stellation pattern on page 97.

External links

• Weisstein, Eric W. "Icositruncated dodecadodecahedron". MathWorld.