Four constituent points of the quadrangle (A, B, C, P)
  Six constituent lines of the quadrangle
  Nine-point conic (a nine-point hyperbola, since P is across side AC)
If P were inside triangle △ABC, the nine-point conic would be a nine-point circle.

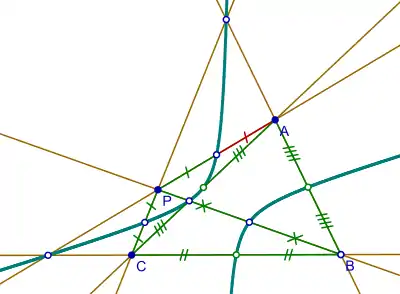
In geometry, the nine-point conic of a complete quadrangle is a conic that passes through the three diagonal points and the six midpoints of sides of the complete quadrangle.

The nine-point conic was described by Maxime Bôcher in 1892.[1] The better-known nine-point circle is an instance of Bôcher's conic. The nine-point hyperbola is another instance.

Bôcher used the four points of the complete quadrangle as three vertices of a triangle with one independent point:

Given a triangle △ABC and a point P in its plane, a conic can be drawn through the following nine points:
the midpoints of the sides of △ABC,
the midpoints of the lines joining P to the vertices, and
the points where these last named lines cut the sides of the triangle.

The conic is an ellipse if P lies in the interior of △ABC or in one of the regions of the plane separated from the interior by two sides of the triangle, otherwise the conic is a hyperbola. Bôcher notes that when P is the orthocenter, one obtains the nine-point circle, and when P is on the circumcircle of △ABC, then the conic is an equilateral hyperbola.

In 1912 Maud Minthorn showed that the nine-point conic is the locus of the center of a conic through four given points.[2]

References

  1. ↑ Maxime Bôcher (1892) Nine-point Conic, Annals of Mathematics, link from Jstor.
  2. ↑ Maud A. Minthorn (1912) The Nine Point Conic, Master's dissertation at University of California, Berkeley, link from HathiTrust.

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.