In chemistry, a radical clock is a chemical compound that assists in the indirect methodology to determine the kinetics of a free-radical reaction. The radical-clock compound itself reacts at a known rate, which provides a calibration for determining the rate of another reaction.
Many organic mechanisms involve intermediates that cannot be identified directly but which are inferred from trapping reactions.[1] When such intermediates are radicals, their lifetimes can be deduced from radical clocks.[2][3] An alternative, perhaps more direct approach involves generation and isolation of the intermediates by flash photolysis and pulse radiolysis, but such methods are time-consuming and require expensive equipment. With an indirect approach of radical clocks, one can still obtain relative or absolute rate constants without the need for instruments or equipment beyond those normally needed for the reaction being studied.[4]
Theory and technique
Radical clock reactions involve a competition between a unimolecular radical reaction with a known rate constant and a bimolecular radical reaction with an unknown rate constant to produce unrearranged and rearranged products. The rearrangement of an unrearranged radical, U•, proceeds to form R• (the clock reaction) with a known rate constant (kr). These radicals react with a trapping agent, AB, to form the unrearranged and rearranged products UA and RA, respectively.[5]
![{\displaystyle {\begin{array}{l}{\ce {U. + AB ->[k_R] {UA}+ B.}}\\{\bigg \downarrow }{k_{r}}\\{\ce {R. + AB -> {RA}+ B.}}\end{array}}}](../I/4abb8b060be8190d61bdb4b7df1812862dca45d4.svg)
The yield of the two products can be determined by gas chromatography (GC) or nuclear magnetic resonance (NMR). From the concentration of the trapping agent, the known rate constant of the radical clock, and the ratio of the products, the unknown rate constant can be indirectly established.
If a chemical equilibrium exists between U• and R•, the rearranged products are dominant.[3] Because the unimolecular rearrangement reaction is first order and the bimolecular trapping reaction is second order (both irreversible), the unknown rate constant (kR) can be determined by:[6]
![{\displaystyle k_{R}={\frac {k_{r}[{\ce {UA}}]}{{\ce {[AB][RA]}}}}}](../I/82eef2a563a3b63951d50036a74666ea862bb854.svg)
Clock rates
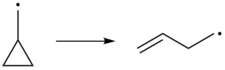
The driving force behind radical clock reactions is their ability to rearrange.[1] Some common radical clocks are radical cyclizations, ring openings, and 1,2-migrations.[3] Two popular rearrangements are the cyclization of 5-hexenyl and the ring-opening of cyclopropylmethyl:[1]
 |
 |
5-hexenyl radical undergoes cyclization to produce a five-membered ring because this is entropically and enthalpically more favored than the six-membered ring possibility.[1][3] The rate-constant for this reaction is 2.3×105 s−1 at 298 K.[5]
Cyclopropylmethyl radical undergoes a very rapid ring opening rearrangement that relieves the ring strain and is enthalpically favorable.[1][3] The rate-constant for this reaction is 8.6×107 s−1 at 298 K.[7]
In order to determine absolute rate constants for radical reactions, unimolecular clock reactions need to be calibrated for each group of radicals such as primary alkyls over a range of time.[3] Through the usage of EPR spectroscopy, the absolute rate constants for unimolecular reactions can be measured with a variety of temperatures.[3][4] The Arrhenius equation can then be applied to calculate the rate constant for a specific temperature at which the radical clock reactions are conducted.
When using a radical clock to study a reaction, there is an implicit assumption that the rearrangement rate of the radical clock is the same as when the rate of that rearrangement reaction rate is determined. A theoretical study of the rearrangement reactions of cyclobutylmethyl and of 5-hexenyl in a variety of solvents found that their reaction rates were only very slightly affected by the nature of the solvent.[5]
The rates of radical clocks can be adjusted to increase or decrease by what types of substituents are attached to the radical clock. In the figure below, the rates of the radical clocks are shown with a variety of substituents attached to the clock.[1]
 | ||
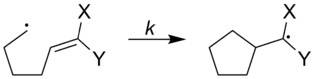| X | Y | k (s−1) |
|---|---|---|
| Ph | Ph | 5x107 |
| OCH3 | H | 1.4x105 |
| OCH3 | CN | 2.5x108 |
| CN | H | 1.6x108 |
By selecting among the general classes of radical clocks and the specific substituents on them, one can be chosen with a rate-constant suitable for studying reactions having a wide range of rates. Reactions having rates ranging from 10−1 to 1012 M−1 s−1 have been studied using radical clocks.[2]
Examples of use
Radical clocks are used in reduction of alkyl halides with sodium naphthalenide, reaction of enones, the Wittig rearrangement,[8] reductive elimination reactions of dialkylmercury compounds, dioxirane dihydroxylations, and electrophilic fluorinations.[3]
References
- 1 2 3 4 5 6 Johnson, C.C.; Lippard, S.J.; Liu, K.E.; Newcomb, M. (1993). "Radical Clock Substrate Probes and Kinetic Isotope Effect Studies of the Hydroxylation of Hydrocarbons by Methane Monooxygenase". J. Am. Chem. Soc. 115 (3): 939–947. doi:10.1021/ja00056a018.
- 1 2 Roschek, B. Jr.; Tallman, K.A.; Rector, C.L.; Gillmore, J.G.; Pratt, D.A.; Punta, C.; Porter, N.A. (2006). "Peroxyl Radical Clocks". J. Org. Chem. 71 (9): 3527–3532. doi:10.1021/jo0601462. PMID 16626136.
- 1 2 3 4 5 6 7 8 Griller, D.; Ingold, K.U. (1980). "Free-radical clocks". Acc. Chem. Res. 13 (9): 317–323. doi:10.1021/ar50153a004.
- 1 2 Moss, R.A.; Platz, M.; Jones, M. Reactive Intermediate Chemistry. Wiley, John & Sons, Incorporated, 2004. 127–128.
- 1 2 3 Fu, Y.; Li, R.-Q.; Liu, L.; Guo, Q.-X. (2004). "Solvent effect is not significant for the speed of a radical clock". Res. Chem. Intermed. 30 (3): 279–286. doi:10.1163/156856704323034012. S2CID 96038335.
- ↑ Newcomb, M. (1993). "Competition Methods and Scales for Alkyl Radical Reaction Kinetics". Tetrahedron. 49 (6): 1151–1176. doi:10.1016/S0040-4020(01)85808-7.
- ↑ Bowry, V.W.; Lusztyk, J.; Ingold, K.U. (1991). "Calibration of a new horologery of fast radical "clocks". Ring-opening rates for ring- and α-alkyl-substituted cyclopropylcarbinyl radicals and for the bicyclo[2.1.0]pent-2-yl radical". J. Am. Chem. Soc. 113 (15): 5687–5698. doi:10.1021/ja00015a024.
- ↑ Garst, John F.; Smith, Calvin D. (March 1976). "Wittig rearrangements of aralkyl alkyl ethers". Journal of the American Chemical Society. 98 (6): 1526–1537. doi:10.1021/ja00422a041. ISSN 0002-7863.