In applied mathematics, Raviart–Thomas basis functions are vector basis functions used in finite element and boundary element methods. They are regularly used as basis functions when working in electromagnetics. They are sometimes called Rao-Wilton-Glisson basis functions.^[1]

The space ${\displaystyle \mathrm {RT} _{q}}$ spanned by the Raviart–Thomas basis functions of order ${\displaystyle q}$ is the smallest polynomial space such that the divergence maps ${\displaystyle \mathrm {RT} _{q}}$ onto ${\displaystyle \mathrm {P} _{q}}$, the space of piecewise polynomials of order ${\displaystyle q}$.^[2]

Order 0 Raviart-Thomas Basis Functions in 2D

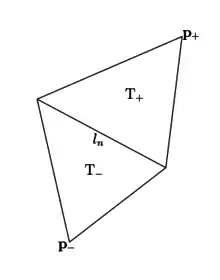
In two-dimensional space, the lowest order Raviart Thomas space, ${\displaystyle \mathrm {RT} _{0}}$, has degrees of freedom on the edges of the elements of the finite element mesh. The ${\displaystyle n}$th edge has an associated basis function defined by^[3]

${\displaystyle \mathbf {f} _{n}(\mathbf {r} )=\left\{{\begin{array}{ll}{\frac {l_{n}}{2A_{n}^{+}}}(\mathbf {r} -\mathbf {p} _{+})\quad &\mathrm {if\ \mathbf {r} \in \ T_{+}} \\-{\frac {l_{n}}{2A_{n}^{-}}}(\mathbf {r} -\mathbf {p} _{-})\quad &\mathrm {if\ \mathbf {r} \in \ T_{-}} \\\mathbf {0} \quad &\mathrm {otherwise} \end{array}}\right.}$

where ${\displaystyle l_{n}}$ is the length of the edge, ${\displaystyle T_{+}}$ and ${\displaystyle T_{-}}$ are the two triangles adjacent to the edge, ${\displaystyle A_{n}^{+}}$ and ${\displaystyle A_{n}^{-}}$ are the areas of the triangles and ${\displaystyle \mathbf {p} _{+}}$ and ${\displaystyle \mathbf {p} _{-}}$ are the opposite corners of the triangles.

Sometimes the basis functions are alternatively defined as

${\displaystyle \mathbf {f} _{n}(\mathbf {r} )=\left\{{\begin{array}{ll}{\frac {1}{2A_{n}^{+}}}(\mathbf {r} -\mathbf {p} _{+})\quad &\mathrm {if\ \mathbf {r} \in \ T_{+}} \\-{\frac {1}{2A_{n}^{-}}}(\mathbf {r} -\mathbf {p} _{-})\quad &\mathrm {if\ \mathbf {r} \in \ T_{-}} \\\mathbf {0} \quad &\mathrm {otherwise} \end{array}}\right.}$

with the length factor not included.

References