Four rectifications

120-cell	Rectified 120-cell
600-cell	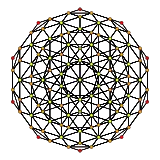Rectified 600-cell
Orthogonal projections in H3 Coxeter plane

In geometry, a rectified 120-cell is a uniform 4-polytope formed as the rectification of the regular 120-cell.

E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC₁₂₀.

There are four rectifications of the 120-cell, including the zeroth, the 120-cell itself. The birectified 120-cell is more easily seen as a rectified 600-cell, and the trirectified 120-cell is the same as the dual 600-cell.

Rectified 120-cell

Rectified 120-cell
Schlegel diagram, centered on icosidodecahedon, tetrahedral cells visible
Type	Uniform 4-polytope
Uniform index	33
Coxeter diagram
Schläfli symbol	t1{5,3,3} or r{5,3,3}
Cells	720 total: 120 (3.5.3.5) 600 (3.3.3)
Faces	3120 total: 2400 {3}, 720 {5}
Edges	3600
Vertices	1200
Vertex figure	triangular prism
Symmetry group	H4 or [3,3,5]
Properties	convex, vertex-transitive, edge-transitive

Net

In geometry, the rectified 120-cell or rectified hecatonicosachoron is a convex uniform 4-polytope composed of 600 regular tetrahedra and 120 icosidodecahedra cells. Its vertex figure is a triangular prism, with three icosidodecahedra and two tetrahedra meeting at each vertex.

Alternative names:

• Rectified 120-cell (Norman Johnson)
• Rectified hecatonicosichoron / rectified dodecacontachoron / rectified polydodecahedron
• Icosidodecahedral hexacosihecatonicosachoron
• Rahi (Jonathan Bowers: for rectified hecatonicosachoron)
• Ambohecatonicosachoron (Neil Sloane & John Horton Conway)

Projections

3D parallel projection
	Parallel projection of the rectified 120-cell into 3D, centered on an icosidodecahedral cell. Nearest cell to 4D viewpoint shown in orange, and tetrahedral cells shown in yellow. Remaining cells culled so that the structure of the projection is visible.

Orthographic projections by Coxeter planes

H4	-	F4
[30]	[20]	[12]
H3	A2 / B3 / D4	A3 / B2
[10]	[6]	[4]

Related polytopes

H4 family polytopes
120-cell	rectified 120-cell	truncated 120-cell	cantellated 120-cell	runcinated 120-cell	cantitruncated 120-cell	runcitruncated 120-cell	omnitruncated 120-cell
{5,3,3}	r{5,3,3}	t{5,3,3}	rr{5,3,3}	t0,3{5,3,3}	tr{5,3,3}	t0,1,3{5,3,3}	t0,1,2,3{5,3,3}
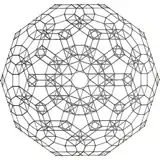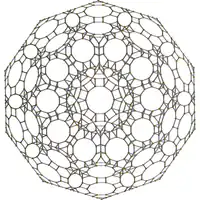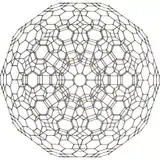600-cell	rectified 600-cell	truncated 600-cell	cantellated 600-cell	bitruncated 600-cell	cantitruncated 600-cell	runcitruncated 600-cell	omnitruncated 600-cell
{3,3,5}	r{3,3,5}	t{3,3,5}	rr{3,3,5}	2t{3,3,5}	tr{3,3,5}	t0,1,3{3,3,5}	t0,1,2,3{3,3,5}

Notes

References

• Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

• Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 33, George Olshevsky.
• rectified 120-cell Marco Möller's Archimedean polytopes in R⁴ (German)
• Klitzing, Richard. "4D uniform polytopes (polychora) o3o3x5o - rahi".
• (in German) Four-dimensional Archimedean Polytopes, Marco Möller, 2004 PhD dissertation
• H4 uniform polytopes with coordinates: r{5,3,3}