Rhombicuboctahedral prism
TypePrismatic uniform polychoron
Uniform index53
Schläfli symbolt0,2,3{3,4,2} or rr{3,4}×{}
s2,3{3,4,2} or s2{3,4}×{}
Coxeter diagram
Cells28 total:
2 rr{4,3} or s2{3,4}
8 {}x{3}
18 {4,3}
Faces100 total:
16 {3}
84 {4}
Edges120
Vertices48
Vertex figure
Trapezoidal pyramid
Symmetry group[4,3,2], order 96
[3+,4,2], order 48
Propertiesconvex

In geometry, a rhombicuboctahedral prism is a convex uniform polychoron (four-dimensional polytope).

It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.

Images


Net
Schlegel diagram
One rhombicuboctahedron and triangular prisms show

Alternative names

  • small rhombicuboctahedral prism
  • (Small) rhombicuboctahedral dyadic prism (Norman W. Johnson)
  • Sircope (Jonathan Bowers: for small-rhombicuboctahedral prism)
  • (small) rhombicuboctahedral hyperprism

Runcic snub cubic hosochoron

Runcic snub cubic hosochoron
Schläfli symbols3{2,4,3}
Coxeter diagram
Cells16 total:
2 t{3,3}
6 {3,3}
8 tricup
Faces52 total:
32 {3}
12{4}
8 {6}
Edges60
Vertices24
Vertex figure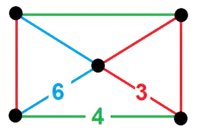
Symmetry group[4,3,2+], order 48
Propertiesconvex

A related polychoron is the runcic snub cubic hosochoron, also known as a parabidiminished rectified tesseract, truncated tetrahedral alterprism, or truncated tetrahedral cupoliprism, s3{2,4,3}, . It is made from 2 truncated tetrahedra, 6 tetrahedra, and 8 triangular cupolae in the gaps, for a total of 16 cells, 52 faces, 60 edges, and 24 vertices. It is vertex-transitive, and equilateral, but not uniform, due to the cupolae. It has symmetry [2+,4,3], order 48.[1][2][3]

It is related to the 16-cell in its s{2,4,3}, construction.

It can also be seen as a prismatic polytope with two parallel truncated tetrahedra in dual positions, as seen in the compound of two truncated tetrahedra. Triangular cupolae connect the triangular and hexagonal faces, and the tetrahedral connect edge-wise between.


Projection
(triangular cupolae hidden)
Net

References

  1. ↑ Klitzing, Richard. "4D tutcup".
  2. ↑ Category S1: Simple Scaliforms Tutcup
  3. ↑ http://bendwavy.org/klitzing/pdf/artConvSeg_8.pdf 4.55 truncated tetrahedron || inverse truncated tetrahedron
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.