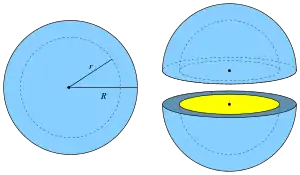
spherical shell, right: two halves

In geometry, a spherical shell is a generalization of an annulus to three dimensions. It is the region of a ball between two concentric spheres of differing radii.^[1]

Volume

The volume of a spherical shell is the difference between the enclosed volume of the outer sphere and the enclosed volume of the inner sphere:

${\displaystyle {\begin{aligned}V&={\tfrac {4}{3}}\pi R^{3}-{\tfrac {4}{3}}\pi r^{3}\\[3mu]&={\tfrac {4}{3}}\pi {\bigl (}R^{3}-r^{3}{\bigr )}\\[3mu]&={\tfrac {4}{3}}\pi (R-r){\bigl (}R^{2}+Rr+r^{2}{\bigr )}\end{aligned}}}$

where r is the radius of the inner sphere and R is the radius of the outer sphere.

Approximation

An approximation for the volume of a thin spherical shell is the surface area of the inner sphere multiplied by the thickness t of the shell:^[2]

${\displaystyle V\approx 4\pi r^{2}t,}$

when t is very small compared to r (${\displaystyle t\ll r}$).

The total surface area of the spherical shell is ${\displaystyle 4\pi r^{2}}$.

See also

• Spherical pressure vessel
• Ball
• Solid torus
• Bubble
• Sphere

References