Topological polymers may refer to a polymeric molecule that possesses unique spatial features, such as linear, branched, or cyclic architectures.[1] It could also refer to polymer networks that exhibit distinct topologies owing to special crosslinkers.[2] When self-assembling or crosslinking in a certain way, polymeric species with simple topological identity could also demonstrate complicated topological structures in a larger spatial scale. Topological structures, along with the chemical composition, determine the macroscopic physical properties of polymeric materials.[3][4]

Definition

Topological polymers, or polymer topology, could refer to a single polymeric chain with topological information or a polymer network with special junctions or connections. When the topology of a polymeric chain or network is investigated, the exact chemical composition is usually neglected, but the way of junctions and connections is more considered. Various topological structures, on one hand, could potentially change the interactions (van der Waals interaction, hydrogen bonding, etc.) between each of the polymer chain. On the other hand, topology also determines the hierarchical structures within a polymer network, from a microscopic level (<1 nm) to a macroscopic level (10-100 nm), which eventually affords polymeric materials with completely different physical properties,[2] such as mechanical property,[5] glass transition temperature,[6] gelation concentration.[7]

Topological polymer classification

In early 1950s, Paul J. Flory was the pioneer who developed theories to explain topology within a polymer network, and the structure-property relationships between the topology and the mechanical property, like elasticity, was initially established afterwards.[3] Later in 1980s, Bertrand Duplantier developed theories to describe any polymer network topologies using statistical mechanics, which could help to derive topology-dependent critical exponents in a polymer network.[8] In early 2000s, Yasuyuki Tezuka and coworkers were the first ones that systematically described a single molecular chain with topological information.[9]

Adapted from Y. Tezuka and coworker's description of a topological polymer chain with more generalized rules,[9] the topology notation rules are to be introduced first, followed by three classical classifications, including linear, branched and cyclic polymer topologies, and they are classified in a table reorganized and redrawn from Y. Tezuka and coworker[9] (Copyright, 2001 by American Chemical Society).

A general polymer chain could be generalized into an undirected graph with nodes (vertices or points) and edges (lines or links) based on graph theory. In a graph theory topology, two sets of nodes are present, termini and junctions. The quantity ‘degree’ represents the number of edges linked to each node, if the degree of a certain node is larger than 3 (including 3), the node is a junction, while the degree of a node is 1, the node is a terminus. There are no nodes with a degree of 2 since they could be generalized into their adjacent nodes.

As for a certain polymer, as long as the topology is fixed, a specific topology notation could be generated using the following rules:

A general polymer chain notation could be expressed as:

  1. Capitalized letter represents the main topology within a polymer, represents linear or branched topology, and Roman numerals are used to represent the number of rings in the polymer chain, represents one cycle, represents two cycles, , , , etc. represents three, four, five cycles and so on.
  2. represents the number of nodes in the graph theory topology, represents the number of termini and represents the number of junctions, and is always true.
  3. If  could represent an exclusive topology, there is no need to add more information to specify the notation. However, if multiple possibilities are present, extra information is needed.

i. For branched topology, a main chain is first selected, and the degree of each junction nodes along the chain should be noted as connected by a hyphen. If there is a side chain on any of the main chain node, should be noted with a bracket following the main chain notation.

ii. For monocyclic topology, the outward branch should be firstly identified with the number of branches at each of the junctions as connected by a hyphen. Then the topology of each branch should be identified using the rule in i as using a bracket following the notations.

iii. For multicyclic topology, superscript letter (, , and so on) is used to describe internal connections within an existing ring.

Linear

Linear topology is a special topological structure that exclusively has two nodes as the termini without any junction nodes. High-density polyethylene (HDPE) could be regarded as a linear polymer chain with very small amount of branching, the linear topology has been listed below:[9] Linear chains capable of forming intra-chain interactions can fold into a wide range of circuit topologies. Examples include biopolymers such as proteins and nucleic acids.

Branched

When side chains are introduced into a linear polymer chain, a branched topology forms. Linear polymers are special types of branched polymers with zero junction nodes, but they are cataloged into two classifications to distinguish their special macroscopic properties.[2] Branched polymers with the same molecular weight usually demonstrate different physical properties due to that branching could generally decrease the van der Waals interactions between each of the polymer chain. Several well-known branched polymers have been synthesized, such as star-shape polymer, comb polymer and dendrimer. Selected branched topologies have been listed below:[9]

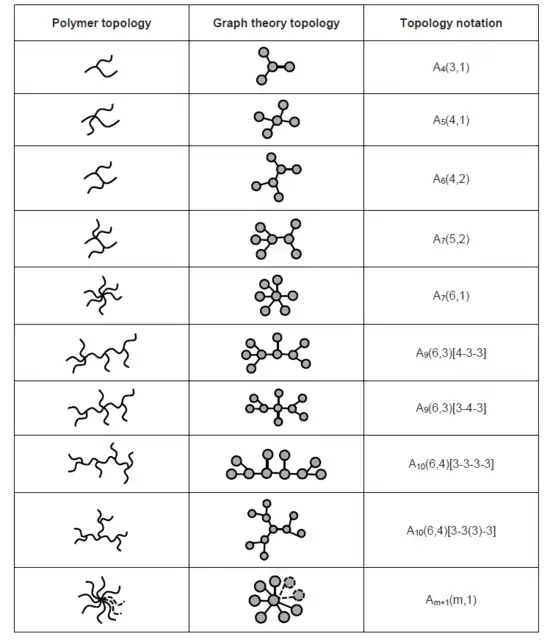
Cyclic

Cyclic structures are of interest topologically because there are no termini in this topology and the physical property could be dramatically different as a result of the restriction of the termini.

Monocyclic

Monocyclic topology is a topological structure with only one cycle in the polymer chain, and it could be coupled with outward branching structures. Selected monocyclic topologies have been listed below:[9]

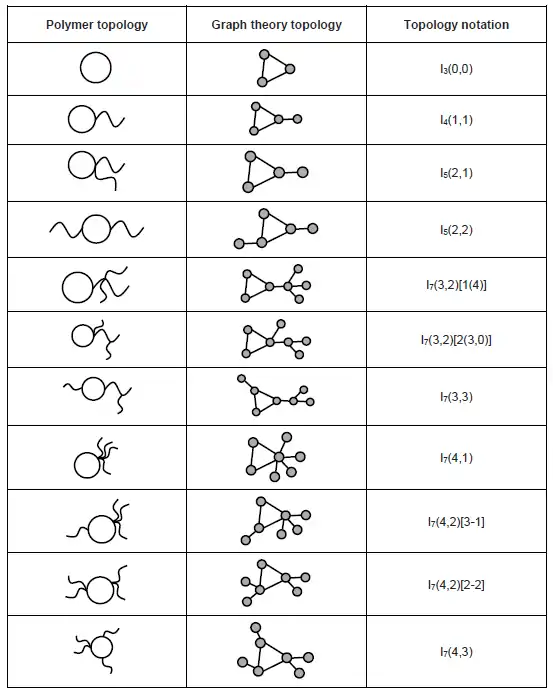
Bicyclic

Bicyclic topology refers to a structure that two cycles connected internally or externally are present in a polymer chain. Selected bicyclic topologies are listed below:[9]

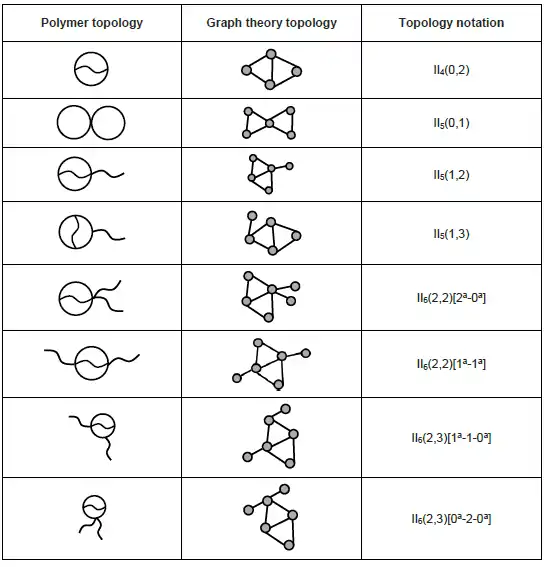
Polycyclic

Similar to monocyclic and bicyclic topologies, polycyclic topologies possess more cycles in a polymer chain and are more synthetically challenging. Selected polycyclic (tricyclic) topologies are listed below:[9]

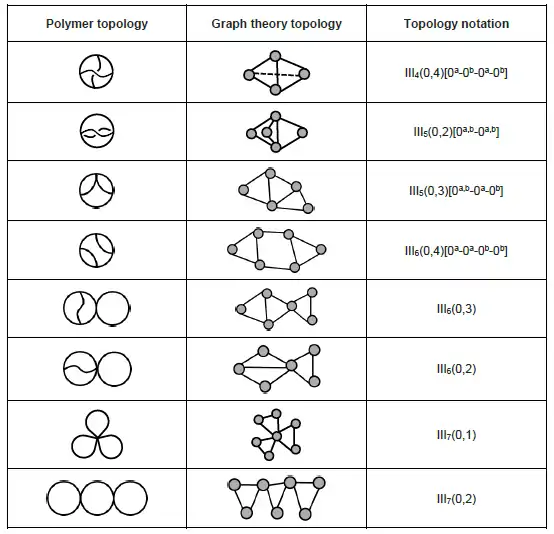
Polymer network topology

Unlike single chain polymeric species, polymer network topology is more complicated as a result of the amorphous feature so that a simple notation is usually not feasible. To analyze the topology of a network, the crosslinkers, including the branched crosslinker and cyclic crosslinker, are considered.

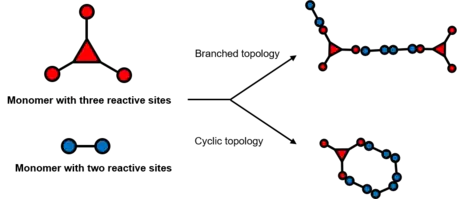
Branched and cyclic topology polymer network formed by monomers with two or three reactive sites.[2]

Branched crosslinking

Branched crosslinkers are entities that do not form cyclic topologies, which could be simply understood by branched topological polymer chain above. The ‘degree’ of branched demonstrates the theoretical number of polymer strands at the junctions of the crosslinker, also known as branch functionality (f).[2]

Combining monomers with different degree of branch functionality could generate various topological network with distinct elastic property. Meanwhile, amphiphilic polymers, such as block copolymers, when forming micelle structures, could also be treated as a branched crosslinker with high degree of branch functionality.

Cyclic crosslinking

Branched crosslinkers should in principle form branched polymer network, but in practice, they could also generate loops and cycles.

Cyclic crosslinkers are more sophisticated and show multiple possibilities. Loops or cycles could form in a smaller scale between two polymer chains or in a larger scale among multiple polymer strands. Besides, bicyclic topology is likely to form if two loops are catenated or linked internally or externally. Special cyclic crosslinking is more attractive within rotaxanes or catenanes since cycles are already present in those molecules.

The characterization of cyclic topologies within a polymer network, compared to branched crosslinker, is relatively harder to perform. Conventional techniques such as rheology and tensile strength analysis are used to offer semiquantitative insights into the polymer topologies.[10] Recently, the development of multiple quantum nuclear magnetic resonance (NMR)[11] and network disassembly spectrometry (NDS)[12] techniques provides quantitative characterizations of loops or cycles in a polymer network.[2]

Topological polymer/network synthesis

Topological polymer single chain

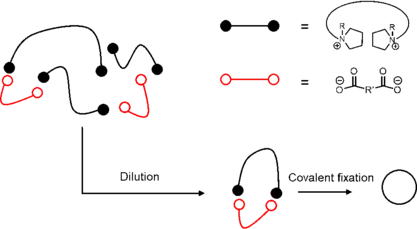
Electrostatic self-assembly and covalent fixation to form a cyclic polymer. Cations and anions self-assemble upon dilution and react with each other upon heat.[13]

The synthesis of branched polymers (grafted polymer, comb polymer, star-shape polymer and dendrimer) has been well developed using well-known polymerization methodology such as cationic/anionic polymerization.[14]

Unlike branched polymer chain synthesis, the synthesis of cyclic polymer is more challenging. General cyclic species involve the combination between two fragments or among several fragments. Electrostatic self-assembly and covalent fixation is one of the most effective strategies to synthesize cyclic topological polymer. The reaction is driven by the electrostatic interactions between telechelic polytetrahydrofurans with cyclic ammonium salt and pluricaboxylate counterions. Upon dilution, the anions and cations could self-assemble into a cyclic structure, followed by a covalent fixation by heat or other external stimuli to undergo ring-opening reaction and close the chain into a cycle.[13]

Topological polymer network

Polymer networks intrinsically have various spatial features due to their amorphous property within a three-dimensional network. There are generally two ways to introduce spatially unique entities into a polymer network:

  • The construction of a topological polymer network using monomer and crosslinker building blocks for a spatial uniqueness.[15]
  • The introduction of crosslinkers that possess topological merits, such as polyrotaxane, polycatenane, daisy chain and so on.[2]

Examples

The topology of a polymer chain or a polymer network is crucial in determining the macroscopic properties of a polymeric material, especially mechanical properties like elasticity and physical properties involving phase transitions. To date, several polymers with topological interest have been developed, which have been used for many applications, such as mechanical elastomer,[16] energy,[17] and so on. Below are some of the representative topological polymers or polymer networks.

Interpenetrating polymer

Interpenetration polymers are polymer networks involving two and more polymer strands which are spatially intertwining with each other to form unique spatial topologies.[18]

Dendrimer

Dendrimer is a special branched polymers with a larger fraction of terminal nodes compared to the junction nodes and could be used for applications in drug delivery[19] or catalysis.[20]

Polyrotaxane

Polyrotaxane is a polymer chain or a polymer network with mechanical interlock structures between ring-like molecules and polymer chain, where both the rings and the linear polymer chain could serve as the crosslinker to form a polymer network.[21]

References

  1. ↑ Tezuka Y, Oike H (July 2002). "Topological polymer chemistry". Progress in Polymer Science. 27 (6): 1069–1122. doi:10.1016/S0079-6700(02)00009-6.
  2. 1 2 3 4 5 6 7 Gu Y, Zhao J, Johnson JA (March 2019). "A (Macro)Molecular-Level Understanding of Polymer Network Topology". Trends in Chemistry. 1 (3): 318–334. doi:10.1016/j.trechm.2019.02.017.
  3. 1 2 Flory PJ (June 1985). "Network topology and the theory of rubber elasticity". British Polymer Journal. 17 (2): 96–102. doi:10.1002/pi.4980170202.
  4. ↑ Wang R, Johnson JA, Olsen BD (March 2017). "Odd–Even Effect of Junction Functionality on the Topology and Elasticity of Polymer Networks". Macromolecules. 50 (6): 2556–2564. Bibcode:2017MaMol..50.2556W. doi:10.1021/acs.macromol.6b01912. ISSN 0024-9297.
  5. ↑ Gu Y, Alt EA, Wang H, Li X, Willard AP, Johnson JA (August 2018). "Photoswitching topology in polymer networks with metal-organic cages as crosslinks". Nature. 560 (7716): 65–69. Bibcode:2018Natur.560...65G. doi:10.1038/s41586-018-0339-0. PMID 30022167.
  6. ↑ Phillips, J.C. (May 1981). "Topology of covalent non-crystalline solids III: Kinetic model of the glass transition". Journal of Non-Crystalline Solids. 44 (1): 17–30. Bibcode:1981JNCS...44...17P. doi:10.1016/0022-3093(81)90129-0.
  7. ↑ Hall CC, Zhou C, Danielsen SP, Lodge TP (2016-03-22). "Formation of Multicompartment Ion Gels by Stepwise Self-Assembly of a Thermoresponsive ABC Triblock Terpolymer in an Ionic Liquid". Macromolecules. 49 (6): 2298–2306. Bibcode:2016MaMol..49.2298H. doi:10.1021/acs.macromol.5b02789. ISSN 0024-9297.
  8. ↑ Duplantier B (February 1989). "Statistical mechanics of polymer networks of any topology". Journal of Statistical Physics. 54 (3–4): 581–680. Bibcode:1989JSP....54..581D. doi:10.1007/BF01019770.
  9. 1 2 3 4 5 6 7 8 Tezuka Y, Oike H (November 2001). "Topological polymer chemistry: systematic classification of nonlinear polymer topologies". Journal of the American Chemical Society. 123 (47): 11570–6. doi:10.1021/ja0114409. PMID 11716710.
  10. ↑ Stadler FJ (May 2013). "Quantifying primary loops in polymer gels by linear viscoelasticity". Proceedings of the National Academy of Sciences of the United States of America. 110 (22): E1972. Bibcode:2013PNAS..110E1972S. doi:10.1073/pnas.1303135110. PMC 3670358. PMID 23633573.
  11. ↑ Lange F, Schwenke K, Kurakazu M, Akagi Y, Chung UI, Lang M, Sommer JU, Sakai T, Saalwächter K (2011-12-27). "Connectivity and Structural Defects in Model Hydrogels: A Combined Proton NMR and Monte Carlo Simulation Study". Macromolecules. 44 (24): 9666–9674. Bibcode:2011MaMol..44.9666L. doi:10.1021/ma201847v. ISSN 0024-9297.
  12. ↑ Zhou H, Woo J, Cok AM, Wang M, Olsen BD, Johnson JA (November 2012). "Counting primary loops in polymer gels". Proceedings of the National Academy of Sciences of the United States of America. 109 (47): 19119–24. Bibcode:2012PNAS..10919119Z. doi:10.1073/pnas.1213169109. PMC 3511143. PMID 23132947.
  13. 1 2 Oike H, Imaizumi H, Mouri T, Yoshioka Y, Uchibori A, Tezuka Y (October 2000). "Designing Unusual Polymer Topologies by Electrostatic Self-Assembly and Covalent Fixation". Journal of the American Chemical Society. 122 (40): 9592–9599. doi:10.1021/ja001736z.
  14. ↑ Yates CR, Hayes W (July 2004). "Synthesis and applications of hyperbranched polymers". European Polymer Journal. 40 (7): 1257–1281. doi:10.1016/j.eurpolymj.2004.02.007.
  15. ↑ Gao H, Matyjaszewski K (April 2009). "Synthesis of functional polymers with controlled architecture by CRP of monomers in the presence of cross-linkers: From stars to gels". Progress in Polymer Science. 34 (4): 317–350. doi:10.1016/j.progpolymsci.2009.01.001.
  16. ↑ Urayama K, Kawamura T, Kohjiya S (January 2009). "Structure–mechanical property correlations of model siloxane elastomers with controlled network topology". Polymer. 50 (2): 347–356. doi:10.1016/j.polymer.2008.10.027.
  17. ↑ Schüler F, Kerscher B, Beckert F, Thomann R, Mülhaupt R (January 2013). "Hyperbranched polymeric ionic liquids with onion-like topology as transporters and compartmentalized systems". Angewandte Chemie. 52 (1): 455–8. doi:10.1002/anie.201205130. PMID 23125048.
  18. ↑ Eddaoudi M, Kim J, Rosi N, Vodak D, Wachter J, O'Keeffe M, Yaghi OM (January 2002). "Systematic design of pore size and functionality in isoreticular MOFs and their application in methane storage". Science. 295 (5554): 469–72. Bibcode:2002Sci...295..469E. doi:10.1126/science.1067208. PMID 11799235. S2CID 39662564.
  19. ↑ D'Emanuele A, Attwood D (December 2005). "Dendrimer-drug interactions". Advanced Drug Delivery Reviews. 57 (15): 2147–62. doi:10.1016/j.addr.2005.09.012. PMID 16310283.
  20. ↑ Crooks RM, Zhao M, Sun L, Chechik V, Yeung LK (March 2001). "Dendrimer-encapsulated metal nanoparticles: synthesis, characterization, and applications to catalysis". Accounts of Chemical Research. 34 (3): 181–90. CiteSeerX 10.1.1.471.3897. doi:10.1021/ar000110a. PMID 11263876.
  21. ↑ Delaviz Y, Gibson HW (September 1992). "Macrocyclic polymers. 2. Synthesis of poly(amide crown ethers) based on bis(5-carboxy-1,3-phenylene)-32-crown-10. Network formation through threading". Macromolecules. 25 (19): 4859–4862. Bibcode:1992MaMol..25.4859D. doi:10.1021/ma00045a005. ISSN 0024-9297.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.