Triangular tiling
Type	Regular tiling
Vertex configuration	3.3.3.3.3.3 (or 36)
Face configuration	V6.6.6 (or V63)
Schläfli symbol(s)	{3,6} {3[3]}
Wythoff symbol(s)	6 | 3 2 3 | 3 3 | 3 3 3
Coxeter diagram(s)	=
Symmetry	p6m, [6,3], (*632)
Rotation symmetry	p6, [6,3]+, (632) p3, [3[3]]+, (333)
Dual	Hexagonal tiling
Properties	Vertex-transitive, edge-transitive, face-transitive

In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.

English mathematician John Conway called it a deltille, named from the triangular shape of the Greek letter delta (Δ). The triangular tiling can also be called a kishextille by a kis operation that adds a center point and triangles to replace the faces of a hextille.

It is one of three regular tilings of the plane. The other two are the square tiling and the hexagonal tiling.

Uniform colorings

A 2-uniform triangular tiling, 4 colored triangles, related to the geodesic polyhedron as {3,6+}_2,0.

There are 9 distinct uniform colorings of a triangular tiling. (Naming the colors by indices on the 6 triangles around a vertex: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314) Three of them can be derived from others by repeating colors: 111212 and 111112 from 121213 by combining 1 and 3, while 111213 is reduced from 121314.^[1]

There is one class of Archimedean colorings, 111112, (marked with a *) which is not 1-uniform, containing alternate rows of triangles where every third is colored. The example shown is 2-uniform, but there are infinitely many such Archimedean colorings that can be created by arbitrary horizontal shifts of the rows.

111111	121212	111222	112122	111112(*)
p6m (*632)	p3m1 (*333)	cmm (2*22)	p2 (2222)	p2 (2222)

121213	111212	111112	121314	111213
p31m (3*3)			p3 (333)

A2 lattice and circle packings

The A^*
₂ lattice as three triangular tilings: + +

The vertex arrangement of the triangular tiling is called an A₂ lattice.^[2] It is the 2-dimensional case of a simplectic honeycomb.

The A^*
₂ lattice (also called A³
₂) can be constructed by the union of all three A₂ lattices, and equivalent to the A₂ lattice.

+ + = dual of =

The vertices of the triangular tiling are the centers of the densest possible circle packing.^[3] Every circle is in contact with 6 other circles in the packing (kissing number). The packing density is π⁄√12 or 90.69%. The voronoi cell of a triangular tiling is a hexagon, and so the voronoi tessellation, the hexagonal tiling, has a direct correspondence to the circle packings.

Geometric variations

Triangular tilings can be made with the equivalent {3,6} topology as the regular tiling (6 triangles around every vertex). With identical faces (face-transitivity) and vertex-transitivity, there are 5 variations. Symmetry given assumes all faces are the same color.^[4]

• 
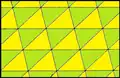  Scalene triangle
  p2 symmetry
• 
  Scalene triangle
  pmg symmetry
• 
  Isosceles triangle
  cmm symmetry
• 
  Right triangle
  cmm symmetry
• 
  Equilateral triangle
  p6m symmetry

Related polyhedra and tilings

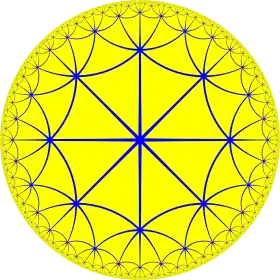
The planar tilings are related to polyhedra. Putting fewer triangles on a vertex leaves a gap and allows it to be folded into a pyramid. These can be expanded to Platonic solids: five, four and three triangles on a vertex define an icosahedron, octahedron, and tetrahedron respectively.

This tiling is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.

*n32 symmetry mutation of regular tilings: {3,n}
Spherical				Euclid.	Compact hyper.		Paraco.	Noncompact hyperbolic
3.3	33	34	35	36	37	38	3∞	312i	39i	36i	33i

It is also topologically related as a part of sequence of Catalan solids with face configuration Vn.6.6, and also continuing into the hyperbolic plane.

V3.6.6

V4.6.6

V5.6.6

V6.6.6

V7.6.6

Wythoff constructions from hexagonal and triangular tilings

Like the uniform polyhedra there are eight uniform tilings that can be based from the regular hexagonal tiling (or the dual triangular tiling).

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms, 7 which are topologically distinct. (The truncated triangular tiling is topologically identical to the hexagonal tiling.)

Uniform hexagonal/triangular tilings
Fundamental domains	Symmetry: [6,3], (*632)							[6,3]+, (632)
	{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}
Config.	63	3.12.12	(6.3)2	6.6.6	36	3.4.6.4	4.6.12	3.3.3.3.6

Triangular symmetry tilings
Wythoff	3 | 3 3	3 3 | 3	3 | 3 3	3 3 | 3	3 | 3 3	3 3 | 3	3 3 3 |	| 3 3 3
Coxeter
Image Vertex figure	(3.3)3	3.6.3.6	(3.3)3	3.6.3.6	(3.3)3	3.6.3.6	6.6.6	3.3.3.3.3.3

Related regular complex apeirogons

There are 4 regular complex apeirogons, sharing the vertices of the triangular tiling. Regular complex apeirogons have vertices and edges, where edges can contain 2 or more vertices. Regular apeirogons p{q}r are constrained by: 1/p + 2/q + 1/r = 1. Edges have p vertices, and vertex figures are r-gonal.^[5]

The first is made of 2-edges, and next two are triangular edges, and the last has overlapping hexagonal edges.

2{6}6 or	3{4}6 or	3{6}3 or	6{3}6 or

Other triangular tilings

There are also three Laves tilings made of single type of triangles:

Kisrhombille 30°-60°-90° right triangles

Kisquadrille 45°-45°-90° right triangles

Kisdeltile 30°-30°-120° isosceles triangles

See also

Wikimedia Commons has media related to Order-6 triangular tiling.

• Triangular tiling honeycomb
• Simplectic honeycomb
• Tilings of regular polygons
• List of uniform tilings
• Isogrid (structural design using triangular tiling)

References

• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
• Grünbaum, Branko & Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65, Chapter 2.9 Archimedean and Uniform colorings pp. 102–107)
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p35
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5

External links

• Weisstein, Eric W. "Triangular Grid". MathWorld.
  • Weisstein, Eric W. "Regular tessellation". MathWorld.
  • Weisstein, Eric W. "Uniform tessellation". MathWorld.
• Klitzing, Richard. "2D Euclidean tilings x3o6o - trat - O2".

Fundamental convex regular and uniform honeycombs in dimensions 2–9
Space	Family	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
E10	Uniform 10-honeycomb	{3[11]}	δ11	hδ11	qδ11
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21