Triangular Dominoes is a variant of dominoes using equilateral triangle tiles, patented by Franklin H. Richards in 1885. Two versions were made: a starter set of 35 unique tiles, with each side numbered from zero to four pips, and an advanced set of 56 unique tiles, with each side numbered from zero to five pips. In both versions, a wild card "boss" tile was included, making 36 and 57 tiles in each complete set, respectively.
Equipment
In his patent, Richards used a three-digit notation, referring to the pips in clockwise order from the side(s) with the lowest value. Richards illustrated the tiles as two unique sets, with pip values subject to the following restrictions:[1]
- Pip counts may be repeated
- Starting from the side with the lowest value and proceeding clockwise, the number of pips on a side is equal to or greater than the prior side
In addition to this marking scheme, Richards added the sum of all pips to the center of the tile.[1]
| Triples | Doubles | Singles | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 000 | 001 | 002 | 003 | 004 | 005 | ||||||
| 111 | 011 | 112 | 113 | 114 | 115 | 012 | 013 | 014 | 015 | ||
| 222 | 022 | 122 | 223 | 224 | 225 | 023 | 024 | 025 | 123 | 124 | 125 |
| 333 | 033 | 133 | 233 | 334 | 335 | 034 | 035 | 134 | 135 | 234 | 235 |
| 444 | 044 | 144 | 244 | 344 | 445 | 045 | 145 | 245 | 345 | ||
| 555 | 055 | 155 | 255 | 355 | 455 | ||||||
Percy Alexander MacMahon showed there were 24 possible combinations when each of the three edges of an equilateral triangle are assigned one of four values, and showed the number of unique pieces that can be made in this way is for unique values.[2]: 2 For , there are 45 unique combinations possible, and for , there are 76 unique combinations; the reduced set of 35 and 56 in Triangular Dominoes, for 0–4 and 0–5 pips, respectively, result from the additional restriction for increasing values around each side of the tiles when counting clockwise. This can be demonstrated by examination of the "singles" tiles: where 012 is a valid sequence in Triangular Dominoes, 021 is not, and so the mirror image of each "singles" pattern is excluded; there are ten excluded patterns for the set of 0–4 pips and twenty for the set of 0–5 pips. By examination, mirror images of the triples and doubles are identical to the original tiles and so these patterns already adhere to the counting-up restriction.
- Selected included and excluded tiles
 0-1-2, included
0-1-2, included 0-2-1, excluded (mirror image of 012)
0-2-1, excluded (mirror image of 012) 0-2-4, included
0-2-4, included 0-4-2, excluded (mirror image of 024)
0-4-2, excluded (mirror image of 024) 0-3-5, included
0-3-5, included 0-5-3, excluded (mirror image of 035)
0-5-3, excluded (mirror image of 035)
These restrictions and resulting tile set of Triangular Dominoes were retained, with markings moved to the corners using Arabic numerals for Triominoes, which was published in 1965.
- Comparison of selected tiles in Triominoes and Triangular Dominoes
 0-1-2 (Triangular Dominoes)
0-1-2 (Triangular Dominoes)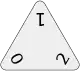 0-1-2 (Triominoes)
0-1-2 (Triominoes) 0-2-4 (Triangular Dominoes)
0-2-4 (Triangular Dominoes)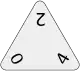 0-2-4 (Triominoes)
0-2-4 (Triominoes) 0-3-5 (Triangular Dominoes)
0-3-5 (Triangular Dominoes)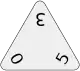 0-3-5 (Triominoes)
0-3-5 (Triominoes)
Gameplay

Richards proposed several games that could be played in the patent.[1]
Points
For this variant, the "boss" tile may be included or left out. The tiles are distributed evenly between the players. Play is led by the player holding the highest triple tile. Each player takes a turn, placing one tile on the table; each tile must be added next to the tile that was placed in the preceding turn, matching the number of pips on adjacent sides. Once one player exhausts their hand, the game is over and the winner's score is determined by the sum of the pips on the tiles remaining in their opponents' hands.[1]
Muggins
This variant is similar to "points", except the matching criterion is the sum of pips on adjacent sides must be a multiple of five.[1]
Star
This variant allows players to lay tiles side-to-side or corner-to-corner. Corner-to-corner plays are allowed when the player is able to match the number on both sides of the corner. If a corner-to-corner match is created, that player can take another turn. Scoring in this variant is accomplished when the sum of all the pips on both dominoes (whether matched side-to-side or corner-to-corner) is a multiple of five;[1] for example, if the 233 and 334 tiles are laid next to each other, the total sum is (2+3+3)+(3+3+4)=18, not divisible by five and hence no score is awarded. Alternatively, if the 233 and 133 tiles are laid next to each other, the total sum is 15, divisible by five, and the player is awarded 15 points.
When the "boss" tile is played, the tile is assumed to have enough pips to bring the sum of it and adjacent tile(s) to a multiple of five. Subsequent tiles played next to the "boss" tile assume the value is zero.[1]
References
- 1 2 3 4 5 6 7 US 331652A, Franklin H. Richards, "Domino", published December 1, 1885
- ↑ MacMahon, P. A. (1921). New Mathematical Pastimes. Cambridge University Press. Retrieved 19 December 2023.
