The Tsou plot is a graphical method of determining the number and nature of the functional groups on an enzyme that are necessary for its catalytic activity.

Theory of Tsou's method

Tsou Chen-Lu^[1] analysed the relationship between the functional groups of enzymes that are necessary for their biological activity and the loss of activity that occurs when the enzyme is treated with an irreversible inhibitor. Suppose now that there are ${\displaystyle n}$ groups on each monomeric enzyme molecule that react equally fast with the modifying agent, and ${\displaystyle n_{\mathrm {essential} }}$ of these are essential for catalytic activity. After modification of an average of ${\displaystyle n_{\mathrm {modified} }}$ groups on each molecule, the probability that any particular group has been modified is ${\displaystyle n_{\mathrm {modified} }/n}$ and the probability that it remains unmodified is ${\displaystyle (1-n_{\mathrm {modified} })^{n_{\mathrm {essential} }}}$. For the enzyme molecule to retain activity, all of its ${\displaystyle n_{\mathrm {essential} }}$ essential groups must remain unmodified, for which the probability is ${\displaystyle 1-n_{\mathrm {modified} }/n}$. The fraction ${\displaystyle f}$ of activity remaining after modification of ${\displaystyle n_{\mathrm {modified} }}$ groups per molecule must be

Tsou plot of data of Paterson and Knowles (1972) for inactivation of pepsin

${\displaystyle f=\left(1-{\dfrac {n_{\mathrm {modified} }}{n}}\right)^{n_{\mathrm {essential} }}}$

and so

${\displaystyle f^{1/n_{\mathrm {essential} }}=1-{\dfrac {n_{\mathrm {modified} }}{n}}}$

This means that a plot of ${\displaystyle f^{1/n_{\mathrm {essential} }}}$ against ${\displaystyle n_{\mathrm {modified} }}$ should be a straight line. As the value of ${\displaystyle n_{\mathrm {essential} }}$ is initially unknown one must draw plots with values 1, 2, 3, etc. to see which one gives a straight line.

There are various complications with this analysis, as discussed in the original paper,^[1] and, more recently in a textbook.^[2]

Experimental applications

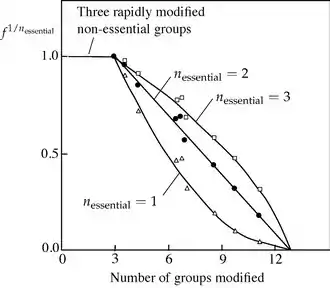
Despite the possible objections, the Tsou plot gave clear results when applied by Paterson and Knowles^[3] to inactivation of pepsin by trimethyloxonium tetrafluoroborate (Meerwein's reagent), a reagent that modifies carboxyl residues in proteins. They were able to deduce from this experiment that three non-essential groups are modified without loss of activity, followed by two essential groups — two because assuming ${\displaystyle n_{\mathrm {essential} }=2}$ yielded a straight line in the plot, whereas values of 1 and 3 yielded curves, with a total of 13 residues modified, as illustrated in the figure.

Tsou's plot has also given good results with other systems, such the type I dehydroquinase from Salmonella typhi,^[4] for which modification of just one essential group by diethyl pyrocarbonate was sufficient to inactivate the enzyme.

Alternative approach to the same question

A little before Tsou published his paper^[1] William Ray and Daniel Koshland had described a different way of investigating the number and nature of groups on an enzyme essential for activity.^[5] Their method depends on kinetic measurements, and cannot be used, therefore, in cases where the modification is too fast for such measurements, such as the case of pepsin^[3] discussed above, but it complements Tsou's approach in useful ways.

Suppose that an enzyme has two groups ${\displaystyle \mathrm {G_{1}} }$ and ${\displaystyle \mathrm {G_{2}} }$ that are both essential for the catalytic activity, so if either is lost the catalytic activity is also lost. If ${\displaystyle \mathrm {G_{1}} }$ is converted to an inactive form in a first-order reaction with rate constant ${\displaystyle k_{1}}$, and ${\displaystyle \mathrm {G_{2}} }$ is inactivated in a first-order reaction with a different rate constant ${\displaystyle k_{2}}$, then the remaining activity ${\displaystyle A}$ after time ${\displaystyle t}$ obeys an equation of the following form:

${\displaystyle A=A_{0}\exp {(-k_{1}t)}\exp {(-k_{2}t)}=A_{0}\exp {[-(k_{1}+k_{2})t]}=A_{0}\exp {(k_{\mathrm {inactivation} }t)}}$

in which ${\displaystyle A_{0}}$ is the value of ${\displaystyle A}$ when ${\displaystyle t=0}$ and ${\displaystyle k_{\mathrm {inactivation} }=k_{1}+k_{2}}$ is the observed first-order rate constant for inactivation, the sum of the rate constants for the separate reactions. The equation can be extended in an obvious way to the case more than two groups are essential. Ray and Koshland also described the properties to be observed when not all of the modified groups are essential.

References