Pure water electrolysis in macrosystem

Pure water in macrosystem cannot be split efficiently due to the lack of rapid ions transport inside bulk solution.

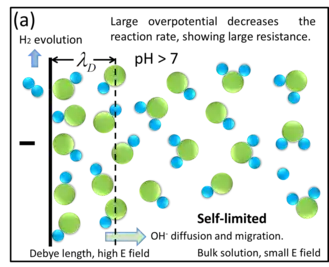
For the analysis of water electrolysis, we shall use H₃O⁺ ions (also known as oxonium ions) at the cathode, as an example to explain the traditional reactions.

Water molecules self-ionize to H₃O⁺ and OH⁻ ions. Near the cathode surface (within the double layer region), newly generated H₃O⁺ ions become hydrogen gas after obtaining electrons from the cathode; however because there is nearly no electric field inside the bulk solution (see section "Electric field distribution"), OH⁻ ions can only transport through the bulk solution very slowly by diffusion. Moreover, in pure water the intrinsic H₃O⁺ concentration is only 10⁻⁷ mol/L, not enough to neutralize the newly generated OH⁻ ions. In this way OH⁻ ions accumulate locally at the cathode surface (turning the solution near cathode into alkaline). Due to Le Chatelier's principle for water self-ionization,

${\displaystyle {\ce {H3O+ + OH- <=> 2H2O}}}$

the OH⁻ ions accumulation impede further self-ionization of the water, which reduces the hydrogen evolution rate and eventually prevents water electrolysis. In this case water electrolysis becomes very slow or even halts; this manifests as a large equivalent resistance between the two electrodes.

This is why in the macrosystem pure water cannot be electrolyzed efficiently - the fundamental reason is the lack of rapid ion transport inside the bulk solution.^[1]

Pure water electrolysis in nanogap cell

In nanogap cell, high electric field in the entire gap can enhance water ionization and mass transport (mainly migration), leading to pure water splitting efficiently limited by electron-transfer.

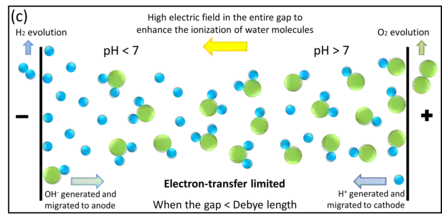
In nanogap cells the high electric field can distribute uniformly across the entire gap (see section "Electric field distribution"). This is different from ion transport in the macrosystem: now newly generated OH⁻ ions can immediately migrate from cathode to anode. In the case where the two electrodes are close enough, the mass transport rate can be even larger than the electron-transfer rate. This results in OH⁻ ions clustering for electron-transfer at the anode, rather than accumulating at the cathode. In this way the entire reaction can keep going and not self-limit.

Notice that for pure water electrolysis in nanogap cells, the net OH⁻ ion accumulation near the anode not only increases the local reactant concentration but also decreases the overpotential requirement (as in the Frumkin effect).^[2] According to Butler–Volmer equation, such ion accumulation increases the electrolysis current, i.e. the water splitting throughput and efficiency.

Thus even pure water can be efficiently electrolyzed, when the electrode gap is small enough.

Virtual breakdown mechanism

In reality water molecule dissociation (the splitting into H₃O⁺ and OH⁻ ions) occurs only at the electrode region (because of the ions continuously consumed at the two electrodes); however it effectively appears that the molecules split in the middle of the gap, with H₃O⁺ ions migrating towards the cathode and OH⁻ ions migrating towards the anode, respectively. The assistance of the huge electric field in the nano-gap (see section "Electric field distribution") not only increases the transport rate but also the water molecules' ionization has been enhanced (i.e. local concentration has been enhanced). Looking from a microscopic perspective, the total effect appears like the breakdown of water molecules.

However this effect is not traditional breakdown, which in fact requires a much larger electric field around 1 V/Å.^[3] In the nanogap cells the huge electric field is still not large enough to split water molecules directly. However it can take advantage of the self-ionization of water, facilitating the equilibrium reaction to shift in the ionization direction.^[1]

${\displaystyle {\ce {2H2O -> H3O+ + OH-}}}$

Such field-assisted ionization, with the fast ion transport (mainly migration), performs very in a similar way to the breakdown of water molecules; that is why this field-assisted effect is named the "virtual breakdown mechanism".

Consider the equation of conductivity,

${\displaystyle \sigma =nq\mu }$

Here the ion charges are not changed. The ion concentration is enhanced but only contributes to the conductivity partially. The fundamental change here is that "apparent mobility" has been significantly enhanced, as the "breakdown" effect. (In traditional electrochemical cells, although the ion intrinsic mobility is high, since there is nearly zero electric field inside bulk solution, it cannot contribute to the conductivity.) Consider the equivalent resistance between the two electrodes, as given by:

${\displaystyle R=\rho {L \over S}}$

When we decrease the gap distance between the two electrodes, not only does the value of L decrease but also the value of resistivity decreases as well; this in fact contributes more to the decrease of the total resistance.^[1]

This "virtual breakdown mechanism" can be applied to almost all kinds of weakly-ionized materials; in fact, such weaker ionization can lead to larger Debye-length inside the solution. At the same size scale it actually helps to achieve the virtual breakdown effect.