The Gougu Theorem diagram added to the Zhoubi by Zhao Shuang
Zhoubi Suanjing
Traditional Chinese《周髀算經》
Simplified Chinese《周髀算经》
Zhoubi
Chinese《周髀》
Literal meaningThe Zhou Gnomon
On Gnomons and Circular Paths
Zhoubi
Traditional Chinese《算經》
Simplified Chinese《算经》
Literal meaningThe Classic of Computation
The Arithmetic Classic

The Zhoubi Suanjing, also known by many other names, is an ancient Chinese astronomical and mathematical work. The Zhoubi is most famous for its presentation of Chinese cosmology and a form of the Pythagorean theorem. It claims to present 246 problems worked out by the early Zhou culture hero Ji Dan and members of his court, placing its contents in the 11th century BC. However, the present form of the book does not seem to be earlier than the 2nd century Eastern Han, with some additions and commentaries continuing to be added for several more centuries.

Names

Zhoubi Suanjing is the atonal pinyin romanization of the modern standard Mandarin pronunciation of the work's Classical Chinese name, 《周髀算經》. The same name has been variously romanized as the Chou Pei Suan Ching,[1] the Tcheou-pi Souane,[2] &c. Its original title was simply the Zhoubi. The character 髀 is a literary term for the femur or thighbone but in context only refers to one or more gnomons, large sticks whose shadows were used for Chinese calendrical and astronomical calculations.[3] Because of the ambiguous nature of the character 周, it has been alternately understood and translated as "On the Gnomon and the Circular Paths of Heaven",[3] the "Zhou Shadow Gauge Manual",[4] "The Gnomon of the Zhou Sundial",[5] and "Gnomon of the Zhou Dynasty".[6] The honorific Suanjing—"Arithmetical Classic",[1] "Sacred Book of Arithmetic",[7] "Mathematical Canon",[6] "Classic of Computations",[8] &c.—was added later.

Dating

Examples of the gnomon described in the work have been found from as early as 2300 BC and Ji Dan, better known as the Duke of Zhou, was an 11th century BC regent and noble during the first generation of the Zhou dynasty. The Zhoubi was traditionally dated to Ji Dan's own life[9] and considered to be the oldest Chinese mathematical treatise.[3] However, although some passages seem to come from the Warring States Period or earlier,[9] the current text of the work mentions Lü Bowei and is believed to have received its current form no earlier than the Eastern Han, during the 1st or 2nd century. The earliest known mention of the text is from a memorial dedicated to the astronomer Cai Yong in 178 CE.[10] It does not appear at all in the Book of Han's account of calendrical, astronomical, and mathematical works, although Joseph Needham allows that this may have been from its current contents having previously been provided in several different works listed in the Han history which are otherwise unknown.[3]

Contents

A umbrella-covered chariot from the terracotta army of the tomb of the First Emperor (2006).

The Zhoubi is an anonymous collection of 246 problems encountered by the Duke of Zhou and figures in his court, including the astrologer Shang Gao. Each problem includes an answer and a corresponding arithmetic algorithm.

It is an important source on early Chinese cosmology, glossing the ancient idea of a round heaven over a square earth (天圆地方, tiānyuán dìfāng) as similar to the round parasol suspended over some ancient Chinese chariots[11] or a Chinese chessboard.[12] All things measurable were considered variants of the square, while the expansion of a polygon to infinite sides approaches the immeasurable circle.[4] This concept of a "canopy heaven" (蓋天, gàitiān) had earlier produced the jade bì (璧) and cóng (琮) objects and myths about Gonggong, Mount Buzhou, Nüwa, and repairing the sky. Although this eventually developed into an idea of a "spherical heaven" (渾天, hùntiān),[13] the Zhoubi offers numerous explorations of the geometric relationships of simple circles circumscribed by squares and squares circumscribed by circles.[14] A large part of this involves analysis of solar declination in the Northern Hemisphere at various points throughout the year.[3]

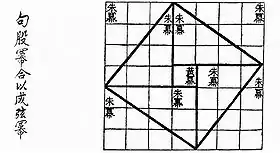
At one point during its discussion of the shadows cast by gnomons, the work presents a form of the Pythagorean theorem known as the gougu theorem (勾股定理, gōugǔ dìnglǐ)[15] from the Chinese names—lit. "hook" and "thigh"—of the two sides of the carpenter or try square.[16] In the 3rd century, Zhao Shuang's commentary on the Zhoubi included a diagram effectively proving the theorem[17] for the case of a 3-4-5 triangle,[18] whence it can be generalized to all right triangles. The original text being ambiguous on its own, there is disagreement as to whether this proof was established by Zhao or merely represented an illustration of a previously understood concept earlier than Pythagoras.[19][15] Shang Gao concludes the gougu problem saying "He who understands the earth is a wise man, and he who understands the heavens is a sage. Knowledge is derived from the shadow [straight line], and the shadow is derived from the gnomon [right angle]. The combination of the gnomon with numbers is what guides and rules the ten thousand things."[20]

Commentaries

The Zhoubi has had a prominent place in Chinese mathematics and was the subject of specific commentaries by Zhao Shuang in the 3rd century, Liu Hui in 263, by Zu Gengzhi in the early 6th century, Li Chunfeng in the 7th century, and Yang Hui in 1270.

See also

References

Citations

  1. 1 2 Needham & al. (1959), p. 815.
  2. ↑ EB, 1st ed. (1771), p. 188.
  3. 1 2 3 4 5 Needham & al. (1959), p. 19.
  4. 1 2 Zou (2011), p. 104.
  5. ↑ Pang-White (2018), p. 464.
  6. 1 2 Cullen (2018), p. 758.
  7. ↑ Davis & al. (1995), p. 28.
  8. ↑ Elman (2015), p. 240.
  9. 1 2 Needham & al. (1959), p. 20.
  10. ↑ Patrick Morgan, Daniel (2 November 2018). "A Radical Proposition on the Origins of the Received Mathematical Classic The Gnomon of Zhou (Zhoubi 周髀)". The Second International Conference on History of Mathematics and Astronomy: 4. Retrieved 25 December 2023.
  11. ↑ Tseng (2011), pp. 45–49.
  12. ↑ Ding (2020), p. 172.
  13. ↑ Tseng (2011), p. 50.
  14. ↑ Tseng (2011), p. 51.
  15. 1 2 Cullen (1996), p. 82.
  16. ↑ Gamwell (2016), p. 39.
  17. ↑ Cullen (1996), p. 208.
  18. ↑ Chemla (2005), p. .
  19. ↑ Chemla (2005).
  20. ↑ Gamwell (2016), p. 41.

Works cited

Further reading

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.