| Uniform octagonal prism | |
|---|---|
 | |
| Type | Prismatic uniform polyhedron |
| Elements | F = 10, E = 24, V = 16 (χ = 2) |
| Faces by sides | 8{4}+2{8} |
| Schläfli symbol | t{2,8} or {8}×{} |
| Wythoff symbol | 2 8 | 2 2 2 4 | |
| Coxeter diagrams | |
| Symmetry | D8h, [8,2], (*822), order 32 |
| Rotation group | D8, [8,2]+, (822), order 16 |
| References | U76(f) |
| Dual | Octagonal dipyramid |
| Properties | convex, zonohedron |
 Vertex figure 4.4.8 | |
In geometry, the octagonal prism is a prism comprising eight rectangular sides joining two regular octagon caps.
Symmetry
| Name | Ditetragonal prism | Ditetragonal trapezoprism |
|---|---|---|
| Image |  |
 |
| Symmetry | D4h, [2,4], (*422) | D4d, [2+,8], (2*4) |
| Construction | tr{4,2} or t{4}×{}, |
s2{2,8}, |
Images
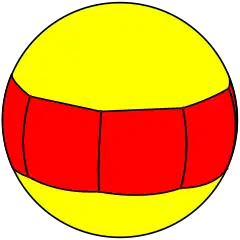
The octagonal prism can also be seen as a tiling on a sphere:
Use
In optics, octagonal prisms are used to generate flicker-free images in movie projectors.
In uniform honeycombs and 4-polytopes
It is an element of three uniform honeycombs:
| Truncated square prismatic honeycomb |
Omnitruncated cubic honeycomb |
Runcitruncated cubic honeycomb |
 |
 |
 |
It is also an element of two four-dimensional uniform 4-polytopes:
| Runcitruncated tesseract |
Omnitruncated tesseract |
 |
 |
Related polyhedra
| Family of uniform n-gonal prisms | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prism name | Digonal prism | (Trigonal) Triangular prism |
(Tetragonal) Square prism |
Pentagonal prism | Hexagonal prism | Heptagonal prism | Octagonal prism | Enneagonal prism | Decagonal prism | Hendecagonal prism | Dodecagonal prism | ... | Apeirogonal prism |
| Polyhedron image | ... | ||||||||||||
| Spherical tiling image | Plane tiling image | ||||||||||||
| Vertex config. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | ... | ∞.4.4 |
| Coxeter diagram | ... | ||||||||||||
| *n42 symmetry mutation of omnitruncated tilings: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| Omnitruncated figure |
 4.8.4 |
 4.8.6 |
 4.8.8 |
 4.8.10 |
 4.8.12 |
 4.8.14 |
 4.8.16 |
 4.8.∞ |
| Omnitruncated duals |
 V4.8.4 |
 V4.8.6 |
 V4.8.8 |
 V4.8.10 |
 V4.8.12 |
 V4.8.14 |
 V4.8.16 |
 V4.8.∞ |
External links
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.