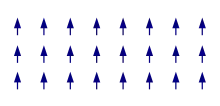
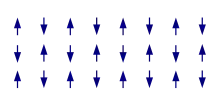

The term magnetic structure of a material pertains to the ordered arrangement of magnetic spins, typically within an ordered crystallographic lattice. Its study is a branch of solid-state physics.
Magnetic structures
Most solid materials are non-magnetic, that is, they do not display a magnetic structure. Due to the Pauli exclusion principle, each state is occupied by electrons of opposing spins, so that the charge density is compensated everywhere and the spin degree of freedom is trivial. Still, such materials typically do show a weak magnetic behaviour, e.g. due to Pauli paramagnetism or Langevin or Landau diamagnetism.
The more interesting case is when the material's electron spontaneously break above-mentioned symmetry. For ferromagnetism in the ground state, there is a common spin quantization axis and a global excess of electrons of a given spin quantum number, there are more electrons pointing in one direction than in the other, giving a macroscopic magnetization (typically, the majority electrons are chosen to point up). In the most simple (collinear) cases of antiferromagnetism, there is still a common quantization axis, but the electronic spins are pointing alternatingly up and down, leading again to cancellation of the macroscopic magnetization. However, specifically in the case of frustration of the interactions, the resulting structures can become much more complicated, with inherently three-dimensional orientations of the local spins. Finally, ferrimagnetism as prototypically displayed by magnetite is in some sense an intermediate case: here the magnetization is globally uncompensated as in ferromagnetism, but the local magnetization points in different directions.
The above discussion pertains to the ground state structure. Of course, finite temperatures lead to excitations of the spin configuration. Here two extreme points of view can be contrasted: in the Stoner picture of magnetism (also called itinerant magnetism), the electronic states are delocalized, and their mean-field interaction leads to the symmetry breaking. In this view, with increasing temperature the local magnetization would thus decrease homogeneously, as single delocalized electrons are moved from the up- to the down-channel. On the other hand, in the local-moment case the electronic states are localized to specific atoms, giving atomic spins, which interact only over a short range and typically are analyzed with the Heisenberg model. Here, finite temperatures lead to a deviation of the atomic spins' orientations from the ideal configuration, thus for a ferromagnet also decreasing the macroscopic magnetization.
For localized magnetism, many magnetic structures can be described by magnetic space groups, which give a precise accounting for all possible symmetry groups of up/down configurations in a three-dimensional crystal. However, this formalism is unable to account for some more complex magnetic structures, such as those found in helimagnetism.
Techniques to study them
Such ordering can be studied by observing the magnetic susceptibility as a function of temperature and/or the size of the applied magnetic field, but a truly three-dimensional picture of the arrangement of the spins is best obtained by means of neutron diffraction.[1][2] Neutrons are primarily scattered by the nuclei of the atoms in the structure. At a temperature above the ordering point of the magnetic moments, where the material behaves as a paramagnetic one, neutron diffraction will therefore give a picture of the crystallographic structure only. Below the ordering point, e.g. the Néel temperature of an antiferromagnet or the Curie-point of a ferromagnet the neutrons will also experience scattering from the magnetic moments because they themselves possess spin. The intensities of the Bragg reflections will therefore change. In fact in some cases entirely new Bragg-reflections will occur if the unit cell of the ordering is larger than that of the crystallographic structure. This is a form of superstructure formation. Thus the symmetry of the total structure may well differ from the crystallographic substructure. It needs to be described by one of the 1651 magnetic (Shubnikov) groups rather than one of the non-magnetic space groups.[3]
Although ordinary X-ray diffraction is 'blind' to the arrangement of the spins, it has become possible to use a special form of X-ray diffraction to study magnetic structure. If a wavelength is selected that is close to an absorption edge of one of elements contained in the materials the scattering becomes anomalous and this component to the scattering is (somewhat) sensitive to the non-spherical shape of the outer electrons of an atom with an unpaired spin. This means that this type of anomalous X-ray diffraction does contain information of the desired type.
More recently, table-top techniques are being developed which allow magnetic structures to be studied without recourse to neutron or synchrotron sources.[4]
Magnetic structure of the chemical elements
Only three elements are ferromagnetic at room temperature and pressure: iron, cobalt, and nickel. This is because their Curie temperature, Tc, is higher than room temperature (Tc > 298K). Gadolinium has a spontaneous magnetization just below room temperature (293 K) and is sometimes counted as the fourth ferromagnetic element. There has been some suggestion that Gadolinium has helimagnetic ordering,[5] but others defend the longstanding view that Gadolinium is a conventional ferromagnet.[6]
The elements Dysprosium and Erbium each have two magnetic transitions. They are paramagnetic at room temperature, but become helimagnetic below their respective Néel temperatures, and then become ferromagnetic below their curie temperatures. The elements Holmium, Terbium, and Thulium display even more complicated magnetic structures.[7]
There is also antiferromagnetic ordering, which becomes disordered above the Néel temperature. Chromium is somewhat like a simple antiferromagnet, but also has an incommensurate spin density wave modulation on top of the simple up-down spin alternation.[8] Manganese (in the α-Mn form) has 29 atoms unit cell, leading to a complex, but commensurate antiferromagnetic arrangement at low temperatures (magnetic space group P42'm').[9][10] Unlike most elements, which are magnetic due to electrons, the magnetic ordering of copper and silver is dominated by the much weaker nuclear magnetic moment, (compare Bohr magneton and nuclear magneton) leading to transition temperatures near absolute zero.[11][12]
Those elements which become superconductors exhibit superdiamagnetism below a critical temperature.
| No. | Name | Superconducting Tc | Curie temperature | Néel temperature |
|---|---|---|---|---|
| 3 | Lithium | 0.0004 K[13] | ||
| 13 | Aluminum | 1.18 K[13] | ||
| 22 | Titanium | 0.5 K[13] | ||
| 23 | Vanadium | 5.4 K[13] | ||
| 24 | Chromium | 311 K[14] | ||
| 25 | Manganese | 100 K[14] | ||
| 26 | Iron | 1044 K[15] | ||
| 27 | Cobalt | 1390 K[15] | ||
| 28 | Nickel | 630 K[15] | ||
| 29 | Copper | 6 * 10−8 K[14] | ||
| 30 | Zinc | 0.85 K[13] | ||
| 31 | Gallium | 1.08 K[13] | ||
| 40 | Zirconium | 0.6 K[13] | ||
| 41 | Niobium | 9.25 K[13] | ||
| 42 | Molybdenum | 0.92 K[13] | ||
| 43 | Technetium | 8.2 K[13] | ||
| 44 | Ruthenium | 0.5 K[13] | ||
| 45 | Rhodium | 0.0003 K[13] | ||
| 46 | Palladium | 1.4 K[13] | ||
| 47 | Silver | 5.6 * 10−10 K[14] | ||
| 48 | Cadmium | 0.52 K[13] | ||
| 49 | Indium | 3.4 K[13] | ||
| 50 | Tin | 3.7 K[13] | ||
| 57 | Lanthanum | 6 K[13] | ||
| 58 | Cerium | 13 K[14] | ||
| 59 | Praseodymium | 25 K[14] | ||
| 60 | Neodymium | 19.9 K[14] | ||
| 62 | Samarium | 13.3 K[14] | ||
| 63 | Europium | 91 K[14] | ||
| 64 | Gadolinium | 293.4 K[15] | ||
| 65 | Terbium | 221 K[15] | 230 K[14] | |
| 66 | Dysprosium | 92.1 K[15] | 180.2 K[14] | |
| 67 | Holmium | 20 K[15] | 132.2 K[14] | |
| 68 | Erbium | 18.74 K[15] | 85.7 K[14] | |
| 69 | Thulium | 32 K[15] | 56 K[14] | |
| 71 | Lutetium | 0.1 K[13] | ||
| 72 | Hafnium | 0.38 K[13] | ||
| 73 | Tantalum | 4.4 K[13] | ||
| 74 | Tungsten | 0.01 K[13] | ||
| 75 | Rhenium | 1.7 K[13] | ||
| 76 | Osmium | 0.7 K[13] | ||
| 77 | Iridium | 0.1 K[13] | ||
| 80 | Mercury | 4.15 K[13] | ||
| 81 | Thallium | 2.4 K[13] | ||
| 82 | Lead | 7.2 K[13] | ||
| 90 | Thorium | 1.4 K[13] | ||
| 91 | Protactinium | 1.4 K[13] | ||
| 92 | Uranium | 1.3 K[13] | ||
| 95 | Americium | 1 K[13] |
References
- ↑ Neutron diffraction of magnetic materials / Yu. A. Izyumov, V.E. Naish, and R.P. Ozerov ; translated from Russian by Joachim Büchner. New York : Consultants Bureau, c1991.ISBN 030611030X
- ↑ A demonstration by Brian Toby
- ↑ Kim, Shoon K. (1999). Group theoretical methods and applications to molecules and crystals (digitally print. 1. paperback version ed.). Cambridge, U.K.: Cambridge University Press. p. 428. ISBN 9780521640626.
- ↑ Mei, Antonio B.; Gray, Isaiah; Tang, Yongjian; Schubert, Jürgen; Werder, Don; Bartell, Jason; Ralph, Daniel C.; Fuchs, Gregory D.; Schlom, Darrell G. (2020). "Local Photothermal Control of Phase Transitions for On-Demand Room-Temperature Rewritable Magnetic Patterning". Advanced Materials. 32 (22): 2001080. arXiv:1906.07239. Bibcode:2020AdM....3201080M. doi:10.1002/adma.202001080. ISSN 1521-4095. PMID 32319146. S2CID 189998035.
- ↑ Coey, J.M.D.; Skumryev, V.; Gallagher, K. (1999). "Is gadolinium really ferromagnetic?". Nature. Springer Science and Business Media LLC. 401 (6748): 35–36. doi:10.1038/43363. ISSN 0028-0836. S2CID 4383791.
- ↑ Kaul, S. N. (2003). "Is gadolinium a helical antiferromagnet or a collinear ferromagnet?". Pramana. Springer Science and Business Media LLC. 60 (3): 505–511. Bibcode:2003Prama..60..505K. doi:10.1007/bf02706157. ISSN 0304-4289. S2CID 56409310.
- ↑ Jensen, Jens; Mackintosh, Allan (1991). Rare Earth Magnetism: Structures and Excitations (PDF). Oxford: Clarendon Press. Retrieved 2020-08-09.
- ↑ Marcus, P M; Qiu, S-L; Moruzzi, V L (1998-07-27). "The mechanism of antiferromagnetism in chromium". Journal of Physics: Condensed Matter. IOP Publishing. 10 (29): 6541–6552. Bibcode:1998JPCM...10.6541M. doi:10.1088/0953-8984/10/29/014. ISSN 0953-8984. S2CID 250905837.
- ↑ Lawson, A. C.; Larson, Allen C.; Aronson, M. C.; Johnson, S.; Fisk, Z.; Canfield, P. C.; Thompson, J. D.; Von Dreele, R. B. (1994-11-15). "Magnetic and crystallographic order in α‐manganese". Journal of Applied Physics. AIP Publishing. 76 (10): 7049–7051. Bibcode:1994JAP....76.7049L. doi:10.1063/1.358024. ISSN 0021-8979.
- ↑ Yamada, Takemi; Kunitomi, Nobuhiko; Nakai, Yutaka; E. Cox, D.; Shirane, G. (1970-03-15). "Magnetic Structure of α-Mn". Journal of the Physical Society of Japan. Physical Society of Japan. 28 (3): 615–627. Bibcode:1970JPSJ...28..615Y. doi:10.1143/jpsj.28.615. ISSN 0031-9015.
- ↑ Huiku, M.T. (1984). "Nuclear magnetism in copper at nanokelvin temperatures and in low external magnetic fields". Physica B+C. Elsevier BV. 126 (1–3): 51–61. Bibcode:1984PhyBC.126...51H. doi:10.1016/0378-4363(84)90145-1. ISSN 0378-4363.
- ↑ Hakonen, P J (1993-01-01). "Nuclear magnetic ordering in silver at positive and negative spin temperatures". Physica Scripta. IOP Publishing. T49A: 327–332. Bibcode:1993PhST...49..327H. doi:10.1088/0031-8949/1993/t49a/057. ISSN 0031-8949. S2CID 250746005.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 G.W. Webb, F. Marsiglio, J.E. Hirsch (2015). "Superconductivity in the elements, alloys and simple compounds". Physica C: Superconductivity and Its Applications. 514: 17–27. arXiv:1502.04724. Bibcode:2015PhyC..514...17W. doi:10.1016/j.physc.2015.02.037. S2CID 119290828.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - 1 2 3 4 5 6 7 8 9 10 11 12 13 14 "Elements handbook: Neel point". Retrieved 27 Sep 2018.
- 1 2 3 4 5 6 7 8 9 "Elements handbook: Curie point". Retrieved 27 Sep 2018.